※当サイトは一部内容を文部科学省、子供たちの未来を育む家庭教育、国立教育政策研究所を参考にしています。お受験プリントのプリントは理英会さんの「ばっちりくんドリル」、こぐま会さんの「ひとりでとっくん」シリーズの補助として活用いただけます。(運営元 : お受験プリント 運営事務局 〒220-0072 神奈川県横浜市西区浅間町1丁目4番3号ウィザードビル)

リアルタイムアクセスのお知らせ!(*300秒毎に更新されます*)
一緒に頑張ろう!




この記事では、私が子供たちに教えた際の経験をもとに、系列/法則性問題の解き方、子供が苦戦したポイント、教えるのに苦労した点、我が家なりの教え方のポイントについて紹介させていただきます。



お受験プリントオリジナルの「全問音声付きプリント」は多くの先輩ママさんたちにご評価いただいてます。ありがとうございます!



youtubeの音声で時間の制限があるなかで練習できたので、本番の試験に向けて本格的に取り組むことができました。ありがとうございました。



本番の試験さながらに様々な問題をyoutubeの音声で解くことができて、力がつきました。時間の区切りがあるということを子供が理解しやすかったと思います。



youtubeの音声を男性、女性と選ぶこともでき、本番の時間に備えることができました。
系列問題は、小学校受験において欠かせない重要なトピックの一つです。
この問題は、子供たちの論理的思考力と問題解決能力を試すもので、しっかりと準備して臨むことが求められます。
私自身、二人の子供たちと一緒に系列問題に取り組む過程で多くの学びと経験を得ることができました。
この記事では、私の経験と、過去に読み込んだ参考資料を基に、系列問題の基本的な解き方、子供たちが苦戦するポイント、教える上での苦労と教え方のポイントについて詳しく解説します。
そして、効果的に学習プロセスを進めるためのアプローチについてもご紹介させていただきます。



記事内容に入る前に、無料プリントのご案内です!
ダウンロード方法はサンプルの下でご案内してます。
反復練習にぜひ、ご活用ください!



お受験プリントは2000名以上の方々にご利用いただいておりますので、ぜひお試しください!(LINEでの宣伝はほとんどしておりませんので、ご安心ください笑)

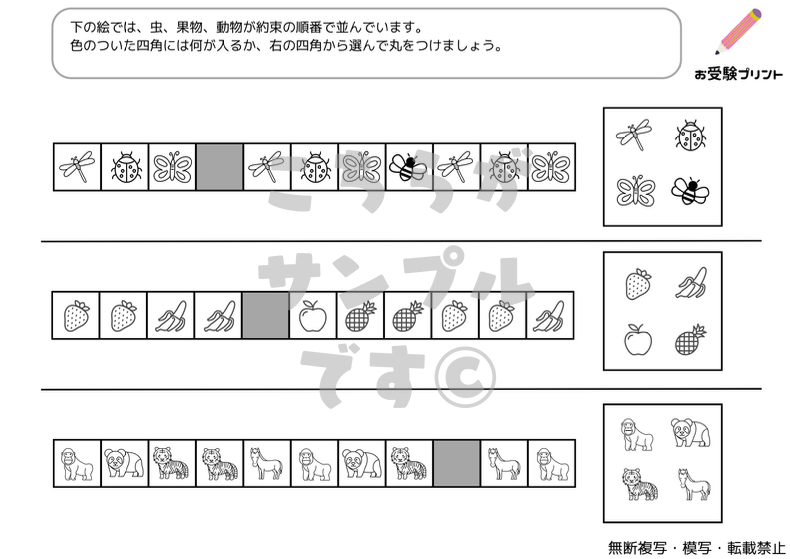
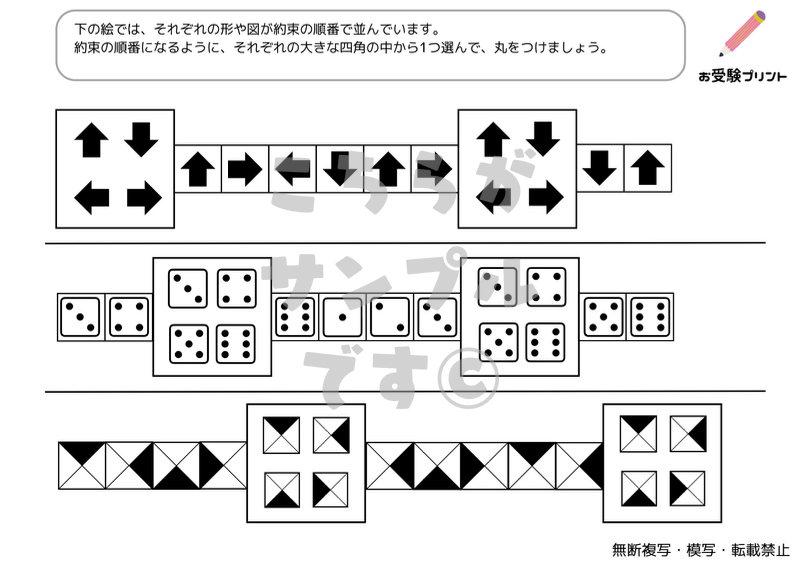
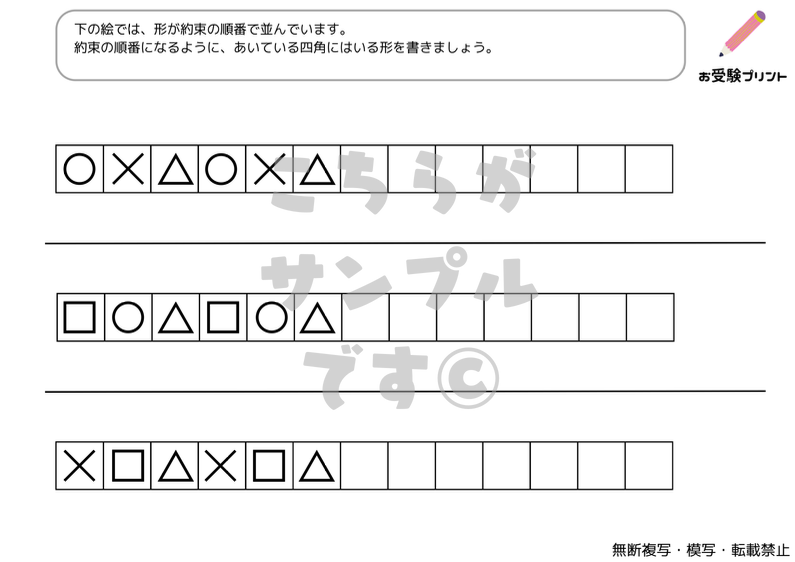
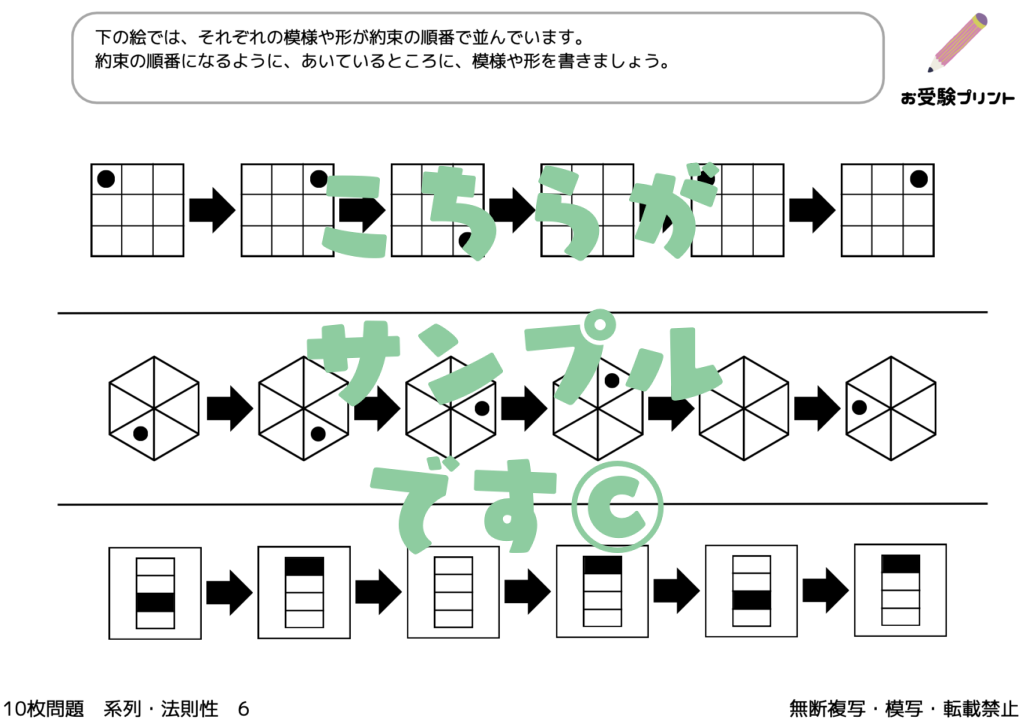
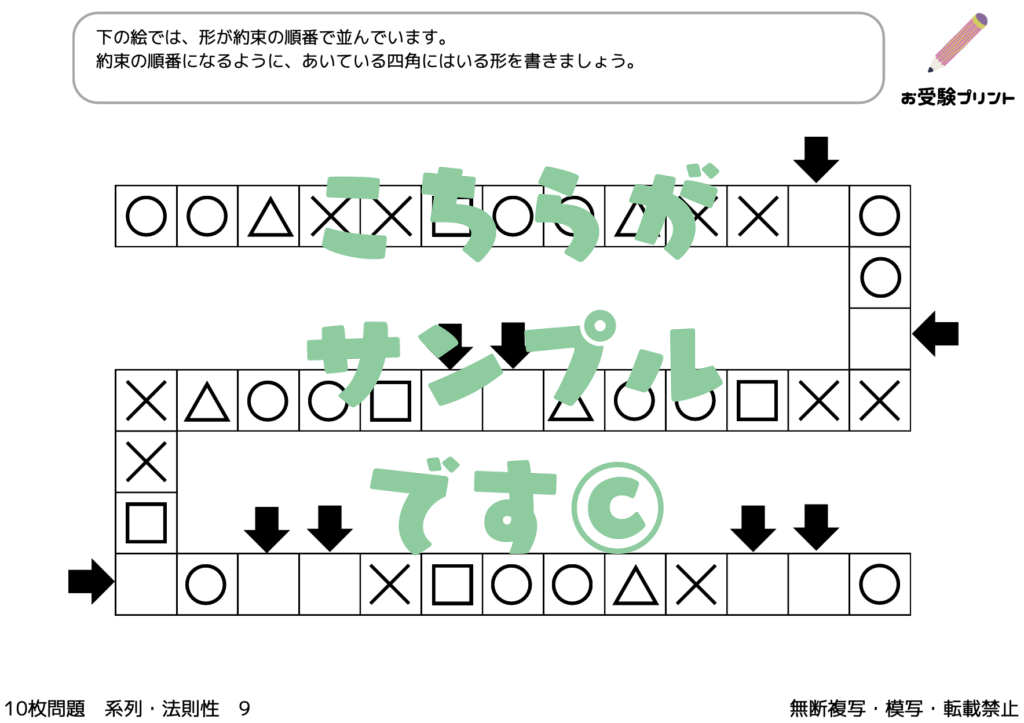
まずはサンプル
サンプルをご覧いただき、ご自宅で使えそうでしたら、ぜひダウンロードに進んでください。(最初の3枚が無料版でダウンロードができます。)
Youtubeショートでも配信中!









簡単3ステップ:3枚無料プリントのダウンロード
お受験プリントの公式LINEアカウントを友だち追加いただいた方に、PDF版の無料プリントをプレゼントしています。



このブログを続けるモチベーションになりますので、ぜひ友だち追加をお願いします!


*写真は「回転図形」のサンプルです。


*パソコンでURLを開くと自動でダウンロード画面になります。
*PDF版の最後には「答え」がついてますが、無料プレゼントしている3枚以外の答えもついています。ご興味いただけましたら、以下のNoteもご覧ください*


無料プリントのURLがLINEアプリで開けないことがあります。
もしも「ページが開けません」というエラーになってしまったら、右下の「・」が3つ並んだボタンをクリックして「ブラウザで開く」をクリックしてください。
プリントを開くことができます。
インスタグラムではサクッとペーパー対策ができる動画を配信しています [フォローはコチラから]


小学校受験の際には、さまざまな知識や技能が試されますが、その中でも系列問題は特に重要だと言われています。
系列問題は、図形や記号などが一定のルールに基づいて並べられ、そのルールを理解し、適切な項目を見つけ出す能力を試す問題です。
この問題を解くことで、子供たちは論理的思考力やパターン認識能力を育むことができます。
これは、小学校受験だけでなく、その後の学習生活においても非常に有用なスキルであり、数学の数列問題などにも繋がる基本的な思考力を培うことができます。
また、系列問題の学習を通して、子供たちに計画的に学習する重要性や、一つ一つの基本をしっかりと理解することの大切さを教えることが出来ます。
例えば、系列問題の解法を学ぶ過程で、子供たちは最初は簡単な問題から始め、徐々に難易度を上げていく方法を学びます。
これは、困難な問題に直面した時にも、基本に立ち返り、一歩一歩解決へと進む姿勢を育むのに役立ちます。
子供たちにとって、系列問題は脳を活性化させ、創造的思考や論理的解析能力を高める良い機会となります。
我が家で初めて系列問題の学習のは、お姉ちゃんがまだ幼稚園の年中さんの時でした。
当初は図形のパターンを理解するのが難しいと感じ、少し戸惑いもありましたが、一緒にルールを見つける練習を続けるうちに、徐々に理解を深めていきました。
弟はお姉ちゃんの経験をもとに、早いうちから系列問題に取り組むことができ、お姉ちゃんが苦労した点や、過去の練習方法を参考にしながら効率的な学習を進めることができました。
系列問題は、一連の図形、記号が特定の規則やパターンに従って並べられ、その規則を理解し、適切な項目を見つけ出す能力を試す問題です。
主に、子供たちに論理的思考力やパターン認識能力を育むことを目的としています。
系列問題の目的は、子供たちに論理的な思考を促し、一連の情報からパターンを抽出し、未知の情報を予測する能力を育てることにあります。これは、日常生活における問題解決の基本的なスキルを学び、また、将来の数学的思考や分析能力の基盤を築くことにも繋がります。
また、系列問題の学習は、子供たちに計画的かつ段階的に学習を進める重要性を教えるためにも非常に効果的です。
例えば、簡単な問題から始めて徐々に難易度を上げていくことで、困難な問題に対しても基本に立ち返り、解法を考える練習ができます。
このように、系列問題は子供たちの思考力を高め、受験準備だけでなく、将来の学習に向けた重要な基盤を築く役割を果たしています。
系列問題は、特定のルールやパターンを理解し、それに基づいて項目を並べる能力を試すため、子供たちにとっては難易度が高い問題となります。
以下に、系列問題が難しいとされる主な理由をいくつかご紹介します。
これらの要因により、系列問題は子供たちにとって難易度が高く、練習と努力が必要とされます。
しかし、これらの困難を乗り越えることで、子供たちは論理的思考力や解決能力を大きく向上させることができます。
また、親としては、子供たちがこれらの困難を乗り越えるプロセスをサポートし、一緒に学ぶ喜びを感じることができます。
系列問題はその内容や形式によって、いくつかの異なる種類に分類されます。
それぞれの種類には特有の特徴や解法があり、子供たちに異なる思考スキルを学ばせることができます。
以下に主な系列問題の種類を挙げています。
図形系列問題は、一連の図形が特定の規則に従って並べられています。子供たちは図形の変化や規則性を理解し、次に来る図形を予測する必要があります。
この種類の問題は、視覚的なパターン認識や図形の理解を深めるのに効果的です。
記号系列問題では、記号の並びや変化の規則を理解することが求められます。記号の変化のパターンを把握し、適切な記号を見つける能力がテストされます。
複合系列問題は、図形、記号などが組み合わさった形で出題される問題で、それぞれの要素の規則を同時に理解する必要があります。これは、子供たちに複雑な思考を要求し、多角的な視点からの問題解決能力を育てます。
これらの系列問題は、子供たちに論理的な思考や規則性の理解、そして多角的な視点を持たせることで、さまざまな問題解決スキルを育てる役割を果たします。
また、それぞれの種類によって求められるスキルが異なるため、幅広い系列問題の学習は子供たちの思考力を全面的に伸ばすことに貢献します。
系列問題はその規則性を見抜き、次の項目を予測することが求められる問題です。
以下に、系列問題を解くための基本的な解き方を説明します。
系列問題を解く基本的なスキルは、子供たちにとっては非常に価値のあるものです。
規則性を理解し、論理的に思考する能力は、受験だけでなく、日常生活や将来の学習においても非常に役立ちます。
そして、親として子供たちと一緒に系列問題を解く時間は、子供たちの思考プロセスを理解し、助ける良い機会となります。
系列問題の練習方法は、子供の理解と技術を向上させるために、効果的で実践的なアプローチが求められます。
まず、系列問題の基本的な概念を理解することが重要で、これには簡単な系列問題から始めることがおすすめです。
基本的な問題を通じて、子供たちは系列の規則やパターンを理解し、次第に複雑な問題に進むことができます。
基本を固めることで、子供たちはより高度な系列問題に対する自信を持つことができ、効果的な学習が期待できます。
次に、反復練習は系列問題の練習方法として非常に重要です。
同じタイプの問題を繰り返し解くことで、子供たちは規則性やパターンをより良く理解し、問題解決の速度を向上させることができます。
また、練習問題のバリエーションを増やし、異なるタイプの系列問題に取り組むことも重要です。
これにより、子供たちはさまざまな系列問題の解法を学び、広範な理解を得ることができます。
さらに、子供に「どうやって考えたのか」を説明させることも、理解を深める助けとなります。
子供が自分の思考過程を言葉で表現することで、理解の確認や、どの部分が理解できていないのかを明確にすることができます。
子供たちが系列問題に取り組む際、最も難しいと感じるポイントの一つが規則性を見つけることです。
これは、幼い子供たちにとってはまだ未熟な論理的思考や抽象的な思考を要求されるため、非常に難しポイントととなることが多いです。
以下に、子供たちが規則性を見つける上で苦戦する主な理由を説明します。
子供たちが規則性を見つける難しさに対処するためには、多くの練習と、親などからの適切な指導が必要です。
系列問題において、最初の項目が空欄になっているタイプの問題は、子供たちにとっては特に難題となることがあります。
このタイプの問題は、規則を逆算する能力や、問題の全体的な構造を理解する力を試すものです。
以下に、このタイプの問題の取り組みにおける主なポイントを説明します。
最初の項目が空欄の問題に対する取り組みは、子供たちの論理的思考力や問題解決能力を大いに発展させる機会となります。
系列問題に取り組む際、基本から学ぶことは非常に重要です。
初めて系列問題に触れる子供たちは、基本的な概念やパターンを理解することが必要で、これには基本から順を追って学習することが求められます。
基本的な知識を固めることで、子供たちは問題の背景やルールを理解し、系列問題の解法を学ぶ土台を築くことができます。
特に、初めての受験を迎えるお姉ちゃんの時、基本から丁寧に指導することで、徐々に困難な問題にも対応できるようになりました。
また、基本からのアプローチは、子供たちが自信を持って問題に取り組む助けとなります。
初めは簡単な問題から始め、徐々に難易度を上げていくことで、子供たちは自分の能力を確信し、新たなチャレンジにも積極的に取り組むことができます。
また、反復練習も重要でした。子供たちには、様々な系列問題を解かせ、それらの問題を通じて得た知識を再確認し、定着させるよう努めました。
特に弟は、お姉ちゃんの経験を参考にして、基本から着実に学習を進め、反復練習を通じて、系列問題の解き方を効果的に理解させることができました。
さらに、基本的な概念を確実に理解しているかをチェックし、必要に応じて補足説明や追加の練習を提供することで、子供たちの理解を深め、問題解決能力を向上させることができます。
基本からのアプローチは、子供たちの学習プロセスを効果的にサポートし、系列問題に対する理解と能力を高める助けとなります。
系列問題は、解き方のパターンとテクニックの選択肢に富んでいる問題分野と言えます。
しかし、これらの多様な解き方やテクニックを適切に教え、子供たちに理解させるのは簡単なことではありません。
以下に、系列問題におけるテクニックと解法の多様性に関する苦労とその重要性について説明します。
系列問題におけるテクニックと解法の多様性は、子供たちにとってはチャレンジングでありながらも、その思考力と論理的思考能力を高める良い機会となります。
親としては、このパターンを理解し、子供たちに適切なアドバイスをすることで、子供たちの系列問題解決能力を大いに向上させることができます。
系列問題は、特定のルールやパターンに基づいて項目が並べられています。
そのため、基本概念の確実な理解は、系列問題を解く第一歩となります。我が家では、まず各項目の関係性や、系列を構成する規則を理解することから始めました。
そして、これらの基本概念をしっかり理解することで、さらに難しい系列問題にも対応できるようになりました。
基本概念を教える際には、実際の問題を利用して視覚的に理解を深めることが重要です。
具体的な問題を示しながら、系列のパターンや規則を明示し、それらを理解することで、子供たちの思考の基盤を築くことができます。
また、基本概念の理解は、子供たちが系列問題の解き方やテクニックを効果的に学ぶための土台となります。
さらに、基本概念の確実な理解は、子供たちが自信を持って問題に取り組む助けとなります。
理解が進むにつれて、子供たちの自信も増し、新たな系列問題に対する挑戦意欲も育まれました。
系列問題の解き方の中で、指さしを利用する方法は我が家では非常に効果的でした。
指さしは、子供たちにとって自然で直感的な動作のため、問題を理解するのに役立っていました。
具体的には、指さしを利用することで、子供たちが系列の各項目を個別に確認し、その関係性を明示的に理解することができます。また、指さしは視覚と連動して作動するため、視覚的な理解を促進し、系列のパターンや規則性を捉えやすくします。
お姉ちゃんと弟が受験対策を進める中で、指さしを利用した解法は特に効果を発揮しました。
子供たちは指を使って系列の項目を指し示し、それにより、項目間の関係性や規則性を明確に理解することができました。また、指さしを利用することで、子供たちは自分自身で系列のパターンを発見し、問題をとく自信を持つようになりました。
また、指差は教える側にとっても非常に有効でした。教える側として子供の思考プロセスを視覚的に把握することができ、どの部分が理解できていて、どの部分が理解できていないのかを明確にすることができるためです。
これにより、子供に対して適切なフィードバックとアドバイスをして、さらなる理解を促すことが可能となります。
系列問題の理解を深め、定着させるには反復練習が不可欠です。
我が家では、毎日一定の時間を設けて系列問題の練習を行うようにしていました。
最初は簡単な問題から始め、徐々に難易度を上げていくことで、子供たちは自身の理解と解法の適用能力を確認し、強化することができました。
反復練習の過程では、間違えた問題に対するフィードバックが重要となります。
間違えた問題を一緒に見直し、何が誤っていたのか、どのように解けば良かったのかを理解することで、子供たちの理解がさらに深まり、次に同様の問題に遭遇した時には正しく解くことができるようになりました。
また、反復練習を通じて、子供たちが自分自身で解き方やテクニックを見つけ、改善する機会も増えました。
特に弟は、自身の解き方を見直し、新しいアプローチを試みることで、さらなる解法の発見に繋がりました。これにより、問題解決の幅が広がり、系列問題の理解がより定着しました。
反復練習による理解の定着は、系列問題の解き方を確固たるものにし、子供たちに自信を与えます。
練習を重ねるごとに、子供たちの解法が洗練され、解決スピードも向上しました。
このように、反復練習は、系列問題の理解を定着させ、子供たちの問題解決能力を高める助けとなるのです。
系列問題は、小学校受験において重要な部分を占め、子供たちの論理的思考力と問題解決能力を鍛える素晴らしい機会となります。
この記事を通じて、私自身が二人の子供たちと一緒に系列問題に取り組んだ経験ご紹介させていただきました。
系列問題を解く基本的なスキルや解き方の理解は、問題への第一歩であり、これにより子供たちはより複雑な問題にも対応できるようになります。
特に、系列問題は子供たちに失敗を恐れずに挑戦する価値を教え、新しい問題や未知の状況に対して柔軟に考える能力を育みます。
反復練習は系列問題のスキルを磨くために欠かせない要素であり、同じタイプの問題を何度も解くことで、子供たちの理解と技術が向上することを確認しました。
指さしを利用した解き方練習は、視覚的サポートを提供し、子供たちの理解を深める助けとなります。
親としては、この方法を効果的に利用し、子供たちの理解と解決能力を向上させることが重要です。系列問題に対する適切な取り組みは、子供たちに粘り強い姿勢と柔軟な思考力を育む貴重な機会となります。
これらの取り組みは、子供たちが未来に向けてさらに困難な課題に対処する基盤を築く助けとなります。
系列問題は、子供たちの成長と学習にとって価値のあるものであり、親が子供たちの学習プロセスをサポートすることで、子供たちの学習経験をより有意義で効果的なものにすることができます。



最後に、系列/法則性問題のプリントを再度ご案内させていただきます!
反復練習にぜひ活用してください!
まずはサンプル
サンプルをご覧いただき、ご自宅で使えそうでしたら、ぜひダウンロードに進んでください。








簡単3ステップ:3枚無料プリントのダウンロード
お受験プリントの公式LINEアカウントを友だち追加いただいた方に、PDF版の無料プリントをプレゼントしています。



このブログを続けるモチベーションになりますので、ぜひ友だち追加をお願いします!


*最後の数字は入力不要です。


*パソコンでURLを開くと自動でダウンロード画面になります。
*PDF版の最後には「答え」がついてますが、無料プレゼントしている3枚以外の答えもついています。ご興味いただけましたら、以下のNoteもご覧ください*
ダウンロードエラーになってしまったら


無料プリントのURLがLINEアプリで開けないことがあります。
もしも「ページが開けません」というエラーになってしまったら、右下の「・」が3つ並んだボタンをクリックして「ブラウザで開く」をクリックしてください。
プリントを開くことができます。

















