※当サイトは一部内容を文部科学省、子供たちの未来を育む家庭教育、国立教育政策研究所を参考にしています。お受験プリントのプリントは理英会さんの「ばっちりくんドリル」、こぐま会さんの「ひとりでとっくん」シリーズの補助として活用いただけます。(運営元 : お受験プリント 運営事務局 〒220-0072 神奈川県横浜市西区浅間町1丁目4番3号ウィザードビル)

リアルタイムアクセスのお知らせ!(*300秒毎に更新されます*)
一緒に頑張ろう!




この記事では、私が子供たちに教えた際の経験をもとに、線対称/対称図形問題の解き方、子供が苦戦したポイント、教えるのに苦労した点、我が家なりの教え方のポイントについて紹介させていただきます。
小学校受験のペーパー試験では、「問題が分かるかどうか」だけでなく、
音声で条件を正確に聞き取れるか
制限時間の中で集中を切らさずに考え続けられるか
途中で迷っても、次の問題へ切り替えられるか といった“試験中の状態”が大きく影響します。
幼児にとって、音声を聞き取りながら条件を整理し、限られた時間の中で考え続けることは、想像以上に負荷のかかる作業です。
早い段階から「本番を意識したテンポや流れ」に触れておくことが、当日の安定感につながります。



お受験プリントオリジナルの「全問音声付きプリント」は多くの先輩ママさんたちにご評価いただいてます。ありがとうございます!



youtubeの音声で時間の制限があるなかで練習できたので、本番の試験に向けて本格的に取り組むことができました。ありがとうございました。



本番の試験さながらに様々な問題をyoutubeの音声で解くことができて、力がつきました。時間の区切りがあるということを子供が理解しやすかったと思います。



youtubeの音声を男性、女性と選ぶこともでき、本番の時間に備えることができました。
小学校受験における数学系問題の中でも、子供たちが苦労しがちな「線対称問題」。
この問題は、子供たちの空間認識能力、論理的思考力、さらには創造性を養う絶好の機会となります。
この記事では、線対称問題の基本から、我が家で子供たちが直面した課題、そしてそれらを効果的に教えるためのポイントについて、私の経験をもとにご紹介します。



記事内容に入る前に、無料プリントのご案内です!
ダウンロード方法はサンプルの下でご案内してます。
反復練習にぜひ、ご活用ください!



お受験プリントは3000名以上の方々にご利用いただいておりますので、ぜひお試しください!(LINEでの宣伝はほとんどしておりませんので、ご安心ください笑)

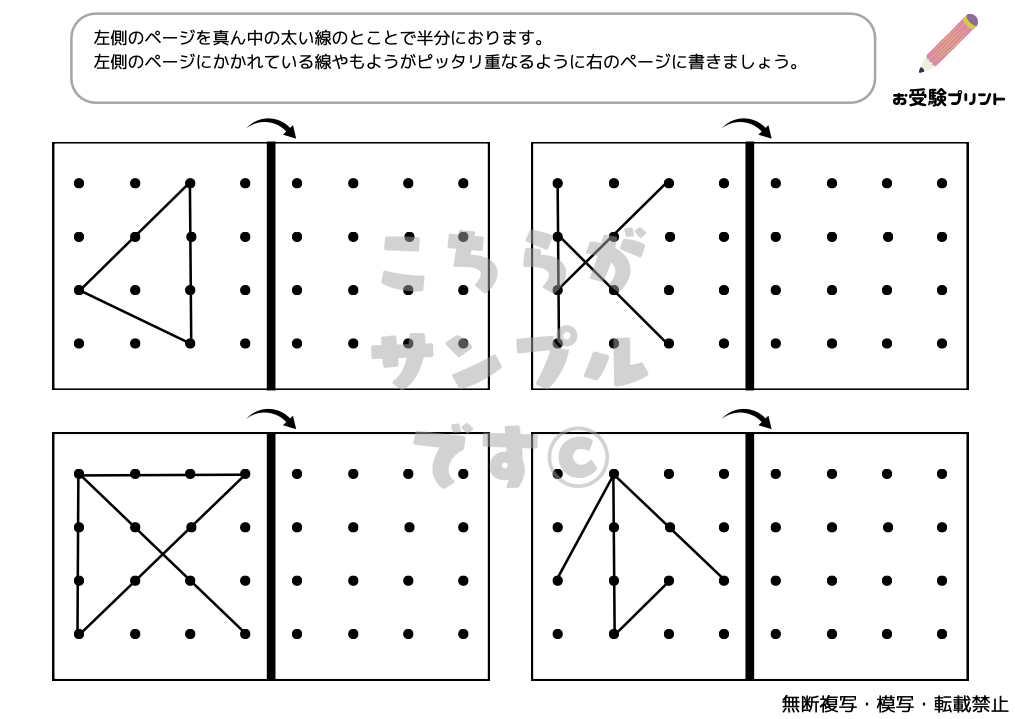
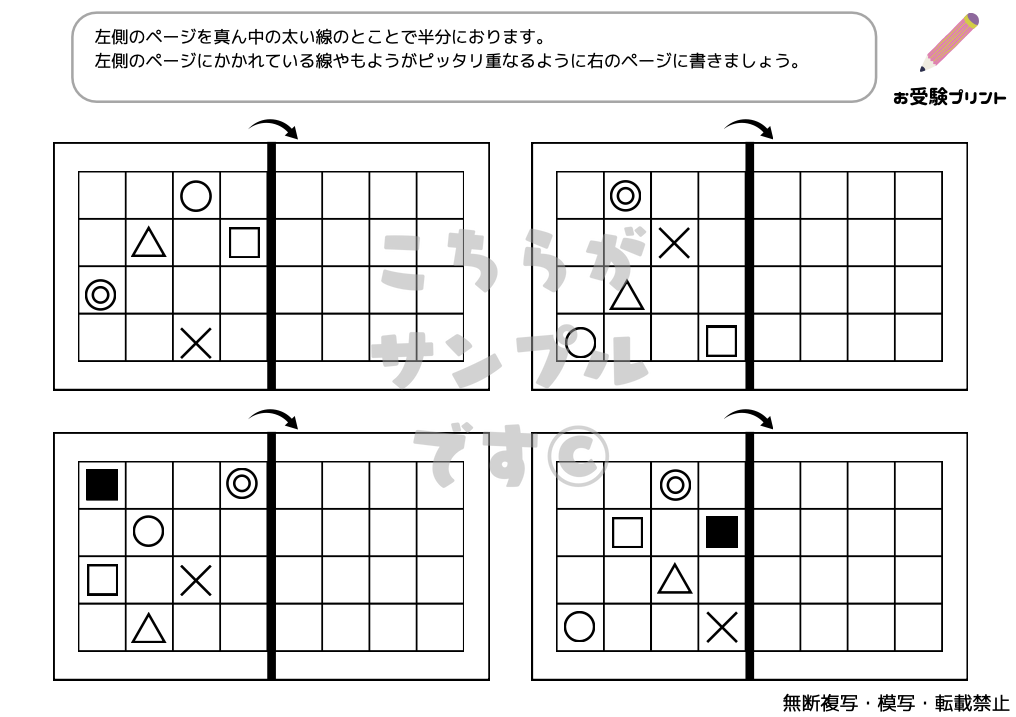
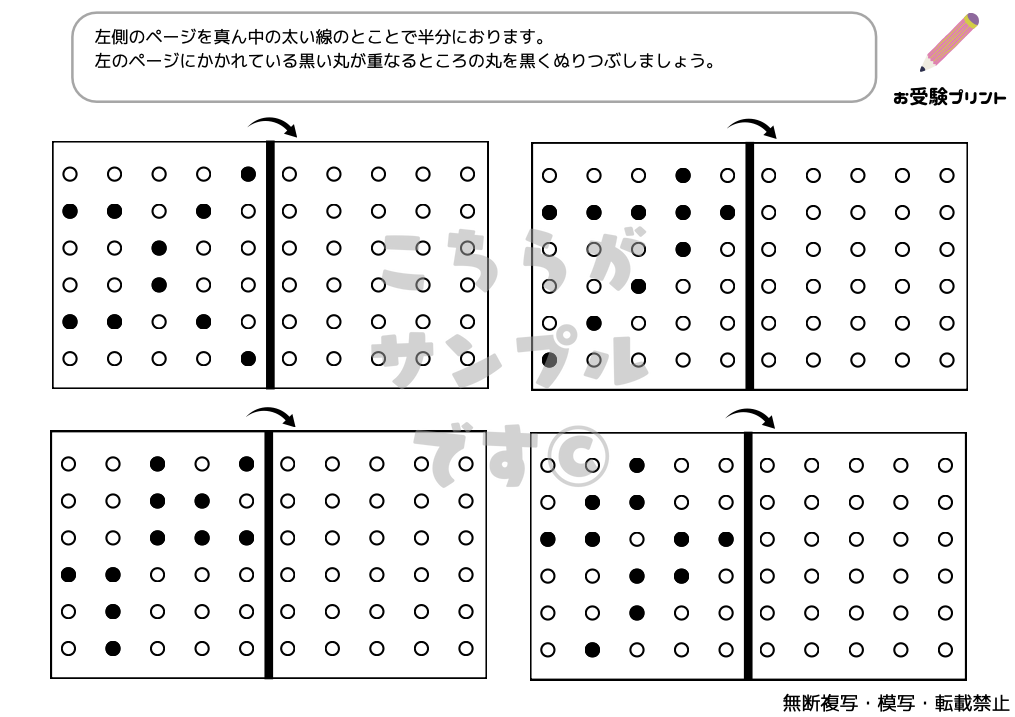
まずはサンプル
サンプルをご覧いただき、ご自宅で使えそうでしたら、ぜひダウンロードに進んでください。(最初の3枚が無料版でダウンロードができます。)
Youtubeショートでも配信中!









簡単3ステップ:3枚無料プリントのダウンロード
お受験プリントの公式LINEアカウントを友だち追加いただいた方に、PDF版の無料プリントをプレゼントしています。



このブログを続けるモチベーションになりますので、ぜひ友だち追加をお願いします!


*写真は「回転図形」のサンプルです。


*パソコンでURLを開くと自動でダウンロード画面になります。
*PDF版の最後には「答え」がついてますが、無料プレゼントしている3枚以外の答えもついています。ご興味いただけましたら、以下のNoteもご覧ください*


無料プリントのURLがLINEアプリで開けないことがあります。
もしも「ページが開けません」というエラーになってしまったら、右下の「・」が3つ並んだボタンをクリックして「ブラウザで開く」をクリックしてください。
プリントを開くことができます。




「線対称問題」は、子供たちの空間認識能力と論理的思考力を測る問題です。
我が家の子供たちが受験した際は、線対称問題は苦労した問題の一つでした。
この種の問題は、一見シンプルですが、実は子供たちにとっては難しい問題です。
なぜなら、単に図形を理解するだけでなく、その図形がどのように空間内で操作されるかを理解する必要があるからです。
我が家の子供たちがこの問題に最初に取り組んだとき、形やサイズ、配置の違いに注意を払う必要があることに苦労しました。
我が家では、お姉ちゃんと弟、二人の子供たちが線対称問題に異なる時期に取り組みました。
お姉ちゃんは、最初から直感的に問題を解くことが得意でしたが、弟は少し苦労しました。
彼にとって、問題を視覚的に理解することが少し難しかったのです。
そこで私たちは、具体的な物を使って線対称を学ぶことにしました。
折り紙を使って、対称軸を中心に図形を折り、その対称性を物理的に示す方法です。
このアプローチは、彼らが視覚的に学ぶことができるので、特に有効でした。
また、実際に手を動かして学ぶことで、彼らはより深く理解を深めることができました。
これらの取り組みは、子供たちが線対称問題をただ解くだけでなく、それを楽しむことにもつながりました。
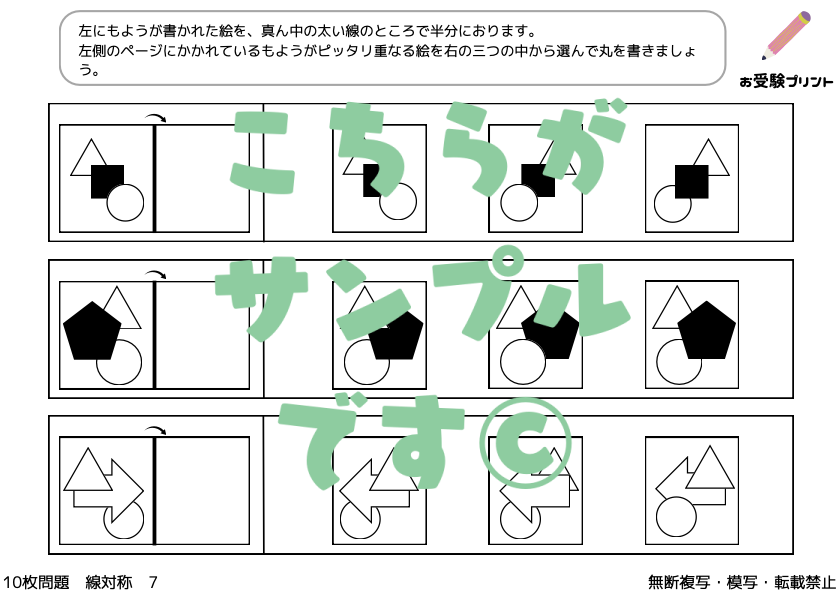
「線対称問題」とは、ある直線(対称軸)を中心にして、図形が左右または上下に完全に重なるように描かれているかを判断する問題です。
この種の問題は、子供たちにとって、形や空間に関する深い理解を必要とします。
線対称問題では、特定の図形が与えられ、その図形が指定された対称軸に関して線対称かどうかを判断しなければなりません。
また、与えられた図形の対称軸を見つけることや、対称軸に沿って新しい図形を作成する問題も出題されます。
これらの問題は、幾何学的な知識だけでなく、視覚的な分析能力も養います。
子供たちは図形を観察し、そのパターンや構造を理解することで、答えに近づくことができます。
このような問題は、子供たちの思考力、問題解決能力、そして創造性を育むのに非常に役立ちます。
「線対称問題」が子供たちにとって難しい理由はいくつかあります。
まず、線対称とは単に形が似ているということではなく、ある特定の軸を中心に完全に重なることを意味します。
この概念を理解するには、図形の形状、サイズ、向きに対する深い理解が必要です。
子供たちは、図形が単に似ているだけではなく、対称軸を中心に完全に一致する必要があることを理解する必要があります。
さらに、線対称問題では図形の各部分がどのように相互に関連しているかを理解する必要があります。
たとえば、図形の一部が対称軸の一方の側にある場合、その正確な鏡像が軸の反対側に存在しなければなりません。
このような空間的関係の認識は、特に幼い子供たちにとっては難しいのです。
さらに、線対称問題を解くには、視覚的な分析スキルと注意力が必要です。
図形を注意深く観察し、細部にまで目を配り、対称軸を正確に特定することは、子供には非常に困難な作業です。
また、対称軸を見つけても、その軸に関して図形が完全に対称であるかを判断することは、さらに高度な思考プロセスを必要とします。
これらの理由から、「線対称問題」は子供たちにとって非常に挑戦的な問題となり、問題を解くためには高度な思考能力と視覚的な分析能力が必要とされます。
これらのスキルは時間と練習を通じて発展しますが、初めのうちは多くの子供たちが苦労するポイントです。
「線対称問題」にはいくつかの異なるタイプがあります。
最も基本的なタイプは、与えられた図形が線対称かどうかを判断する問題です。
このタイプでは、子供たちは図形を観察し、その図形が特定の軸に関して左右対称かどうかを判断する必要があります。
例えば、一般的な幾何学的図形がこのカテゴリに含まれます。
次に、与えられた図形の対称軸を見つける問題があります。
このタイプでは、子供たちは図形を分析し、それがどの軸に関して対称であるかを見つける必要があります。
このプロセスは、図形を精密に観察し、それがどのように折りたたまれるかを想像する能力が求められます。
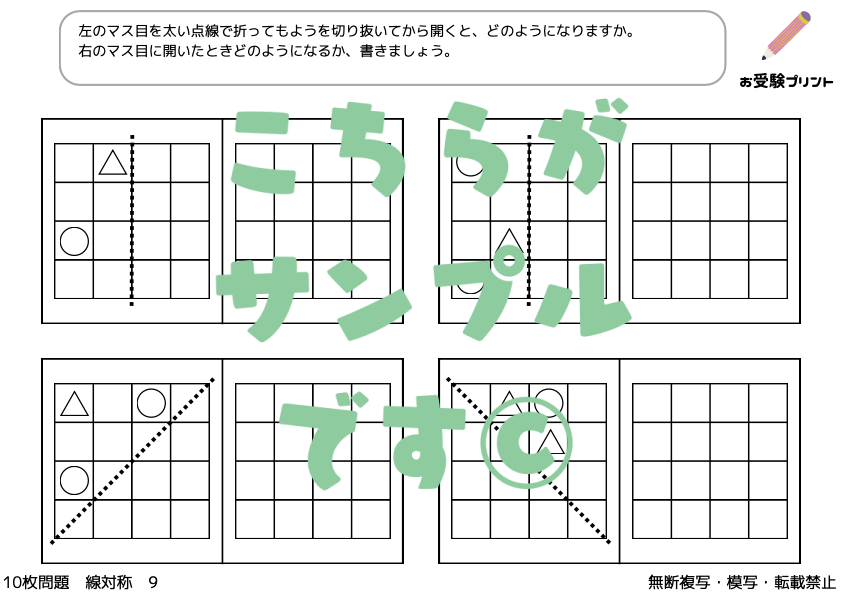
また、与えられた図形を使って新しい線対称な図形を作成する問題もあります。
このタイプの問題では、子供たちは元の図形を利用して、対称軸を中心に新しい図形を描かなければなりません。
これは創造性と空間認識能力が求められる作業です。
さらに進んだレベルの問題では、複数の図形が組み合わされ、それらが全体として線対称を成しているかを判断することを求められることもあります。
これらの問題では、図形の各部分がどのように相互作用するかを理解することが重要です。
線対称問題は単に幾何学的な理解を超えて、子供たちの空間認識能力、注意力、創造性を養うための優れた問題です。
線対称問題を解く基本的な方法は、まず図形とその対称軸を正確に理解することから始まります。
子供たちがこれらの問題に取り組む際、最初に教えるべきは、線対称とは一つの軸に沿って、図形の一方がもう一方の完全な鏡像であるということです。
この概念を理解するために、簡単な図形から始めることが重要です。
次に、対称軸を見つける練習をします。
これは、図形の中心を見つけ、図形を折りたたんだときに完全に一致するかどうかを判断することによって行います。このステップでは、折り紙や鏡を使うことが特に有効です。
子供たちに折り紙を折らせ、折り目が対称軸となるようにし、折り目を中心に図形がどのように一致するかを視覚的に学びます。
また、子供たちに、図形を紙の上に描かせて、対称軸に沿って切り取る練習も有効です。
これにより、子供たちは対称軸の位置をより具体的に理解することができます。
切り取った図形を折りたたんで、完全に一致するかどうかを確認します。
これらの基本的な練習を通じて、子供たちは線対称の概念を徐々に理解し、より複雑な図形や問題に取り組む準備が整います。
線対称問題を解く際の鍵は、図形の対称性を視覚的に捉え、対称軸を正確に特定することにあります。このプロセスを通じて、子供たちは空間認識能力を養い、幾何学的な思考を深めることができます。
「線対称問題」を効果的に練習するためには、いくつかの異なるアプローチがあります。
まず、実物の対象物を使って対称性を観察する方法があります。
例えば、葉や花、家の窓など、日常生活の中で対称性を見つけることができる物を使います。
子供たちにこれらの物を見せ、対称軸を見つけさせることで、彼らは自然界や周囲の世界における対称性の概念を理解するのに役立ちます。
次に、折り紙や紙を使った活動も非常に有効です。
子供たちに紙を折らせ、折り目が対称軸になるようにし、その折り目を中心に図形がどのように一致するかを視覚的に示します。
また、紙を半分に切って、一方をミラーイメージとして他方に描かせることも、対称性の理解を深めるのに役立ちます。
さらに、線対称に関連する様々な種類の問題を解く練習も重要です。
これらの練習方法を通じて、子供たちは線対称の概念を徐々に理解し、より複雑な問題が解けるようになります。
線対称問題の練習は、子供たちの幾何学的思考能力を養い、空間認識能力を高めるための重要なステップです。
線対称問題において、我が子たちが最も苦労したのは、図形の対称性を視覚的に理解することでした。
特に年少の子供たちは、図形の形状やパターンを目で追い、それが対称軸に関してどのように映るかを想像するのが難しいと感じることが多いです。
この問題を解決するために、私たちはまず、単純な形から始めました。
例えば、正方形や円などの基本的な図形を使って、対称軸を理解する練習をしました。
これらの単純な図形を使用することで、子供たちは徐々に、より複雑な図形に対する視覚的な分析能力を発展させることができました。
また、実際に紙を折ったり、鏡を使ったりして、対称性を具体的に示す活動も行いました。
これらの実践的なアプローチは、子供たちが視覚的に対称性を捉えるのを助けるだけでなく、対称軸がどのように機能するかを理解する上でも非常に役立ちました。
しかし、初めのうちは、細かい詳細や複雑な図形における対称性を見分けるのが難しく、何度も繰り返し練習する必要がありました。
このプロセスを通じて、子供たちは図形をより注意深く観察し、その特徴やパターンを認識するスキルを養うことができました。
視覚的な理解は時間と練習を要するプロセスですが、これが成功すると、子供たちはより自信を持って線対称問題に取り組むことができるようになります。
線対称問題におけるもう一つの大きな挑戦は、複雑な図形との対峙です。
基本的な図形、例えば円や正方形などは、比較的対称性が理解しやすいですが、複雑な図形や不規則な形状の場合、子供たちはより多くの困難に直面しました。
これらの図形では、対称軸の特定がより複雑になり、図形の各部分がどのように互いに関連しているかを理解する必要があります。
我が家の子供たちは、特に星形や複数の図形が組み合わさったデザインなど、複数の対称軸を持つ図形に苦労しました。
これらの図形では、どの軸が対称性を保っているのかを見極めるのが難しく、試行錯誤が必要でした。
このような図形を理解するために、私たちは徐々に図形の複雑さを増やしていき、子供たちが一つずつ対処できるようにしました。
また、複雑な図形に取り組む際には、視覚的な分析だけでなく、図形を分割して小さな部分に分けるというアプローチも有効でした。
図形の一部分を取り出し、それがどのように全体の対称性に寄与しているかを理解することで、子供たちは全体の図形に対する理解を深めることができました。
この段階で重要なのは、子供たちが困難に直面したときに諦めず、異なる角度から問題にアプローチすることを学ぶことです。
複雑な図形との対峙を通じて、子供たちはより高度な空間認識能力と問題解決スキルを発展させることができます。
線対称問題を解く過程で、子供たちが直面するもう一つの主要な課題は、論理的思考の発展です。
線対称問題は、単に図形を視覚的に分析するだけでなく、その構造を論理的に理解する必要があります。
特に、複雑な図形や複数の対称軸を持つ問題では、子供たちは一歩引いて図形全体の構造を把握し、どの部分がどのように関連しているかを考える必要があります。
我が家子供たちも、最初はこのような問題に苦労しました。
彼らは図形の一部に焦点を当てすぎたり、対称性を見落としたりすることがありました。
そこで私たちは、図形を分析する際には全体的な視点を持つことの重要性を強調しました。
また、どのようにして特定の図形が対称軸に関して対称になっているかを論理的に説明する練習をしました。
この過程では、子供たちが自分の答えに対して理由を述べることを求めました。
例えば、「この図形はなぜ線対称なのか?」や「なぜこの線が対称軸なのか?」といった質問を通じて、彼らの思考プロセスを明確にしました。
このアプローチは、子供たちが単に正解を見つけるだけでなく、その理由を理解し、論理的に説明する能力を養うのに役立ちました。
論理的思考の発展は、線対称問題に限らず、数学やその他の科目においても非常に重要です。
子供たちがこのスキルを磨くことで、より複雑な問題にも柔軟かつ効果的に対応することができるようになります。
線対称問題を教える上で最も難しかったのは、理論と実践の間のギャップを埋めることでした。
子供たちは、線対称の理論的な概念を理解するのに苦労し、それを実際の問題に適用するのがさらに難しいと感じました。
たとえば、対称軸が何であるか、またそれがどのように図形の対称性に影響を与えるかの概念を説明することは、抽象的な概念を具体的に示す必要があるため、特に難しかったです。
この問題に対処するために、私は子供たちに対して、線対称の基本原則を繰り返し説明し、実際の図形を用いてそれを実践する機会を多く提供しました。
具体的な例を示すことで、子供たちは理論をより深く理解し、それを実際の問題を解く際に活用する方法を学びました。
また、視覚的なエイド、例えば折り紙や鏡を使用して、対称性の概念をより具体的に示しました。
教える過程で大切だったのは、理論的な説明と実際の実践を結びつけることでした。
これにより、子供たちは抽象的な概念をより具体的に捉え、実際の問題に適用する能力を身につけることができました。
線対称問題を教える上で直面したもう一つの挑戦は、視覚的な説明の難しさでした。
対称性は、しばしば視覚的に捉える必要がある概念ですが、これを言葉で説明し、子供たちに理解させるのは容易ではありませんでした。
特に複雑な図形や多角形の場合、その対称性を言葉だけで説明するのはほぼ不可能で、子供たちが視覚的に理解することが重要でした。
この問題を解決するために、私は具体的なツールやアクティビティを利用しました。
例えば、折り紙や鏡を使って対称性を直接示し、子供たちが自ら対称軸を見つけて体験すること繰り返しました。
また、線対称の問題を解く際には、実際に図形を描かせ、対称軸を実際に引いてみるなどのアクティビティを取り入れました。
さらに、視覚的な例を豊富に用いることで、子供たちがより効果的に学ぶことができるようにしました。
例えば、線対称な図形の例を多く示し、それらがどのように対称性を持っているかを解説しました。
このような視覚的なサポートは、子供たちが対称性の概念をより深く理解するのに役立ちました。
視覚的な説明の難しさを克服することは、子供たちが線対称問題をより効果的に理解し、解決するために重要です。
このアプローチは、子供たちの視覚的な学習能力を活用し、より深い理解と実践的な応用を促します。
線対称問題を教える上でのもう一つの課題は、子供たちの持続的な興味とモチベーションを維持することでした。
線対称問題は、理解するのが難しく、時には反復練習が必要なため、子供たちが興味を失いやすい問題の一つです。
特に、理論的な部分が多いときや、繰り返し同じタイプの問題を解くとき、子供たちは飽きやすくなります。
これに対処するために、私は学習を楽しくする方法を常に探しました。
例えば、線対称問題をゲームやクイズ形式で行うことで、学習プロセスに楽しさを加えました。
さらに、小さな達成ごとに褒めることで、彼らの自信を高め、興味を持続させることができました。
また、新しいタイプの問題を定期的に導入することで、学習に新鮮さを持たせ、飽きさせないよう努めました。
子供たちの興味を維持することは、彼らが学習内容に集中し、長期的に知識を習得するために非常に重要です。
楽しさと新鮮さを学習プロセスに取り入れることで、子供たちはより積極的に学び、問題解決能力を高めることができます。
線対称問題の勉強において、最も重要だったのは各子供の個々の学習スタイルと能力に合わせた個別化されたアプローチを取ることでした。
例えば、お姉ちゃんは視覚的な説明と実践的な問題解決を通じてすぐに概念を理解できる傾向がありましたが、弟の方はより具体的な例や実践的な活動を必要としました。
この違いを理解することで、私はそれぞれのニーズに合わせた教育プランを作成しました。
お姉ちゃんには、図形とその対称軸を示す図解や、論理的な問題解決を促す問題を用意しました。
一方、弟には折り紙や図形を切り取る活動など、より実践的なアプローチを採用しました。これにより、彼は対称性の概念をより直感的に理解することができました。
また、それぞれの進捗に合わせて教材の難易度を調整し、子供たちが飽きずに学べるようにしました。
この個別化されたアプローチは、子供たちがそれぞれのペースで学習内容を理解し、習得することを可能にしました。
個々の理解度と興味に合わせて教えることは、効果的な学習経験を提供する上で非常に重要です。
線対称問題の勉強では、視覚的ツールの活用が重要な役割を果たしました。
子供たちが抽象的な概念を理解するのを助けるために、具体的な視覚的ツールを用いることは、学習プロセスを大いに豊かにしました。
たとえば、折り紙を使って対称軸を物理的に示す活動は、子供たちに対称性の概念をより直感的に理解させるのに役立ちました。
図形を実際に折ることで、対称軸がどのように機能するかを視覚的に捉えることができました。
また、鏡を使って対称性を示す活動も効果的でした。
子供たちは、鏡を使って図形の反対側を映し出し、対称性を視覚的に確認することができました。
この方法は、対称軸を理解するのに特に有効で、子供たちが対称性を目で見て理解するのに役立ちました。
視覚的な魅力がある教材は、子供たちの注意を引きつけ、より長く学習に集中させることができました。
視覚的ツールの使用は、子供たちが図形や空間に関する概念を理解し、記憶するのを助けました。
これらのツールは、教育プロセスをよりインタラクティブで理解しやすくし、子供たちの学習経験をより豊かにしました。
視覚的な方法で教えることは、子供たちが線対称問題に対する理解を深めるのに非常に有効です。
線対称問題の教育において、子供たちの創造性を刺激し、興味を引き出すために創造的な教材の使用が非常に重要でした。
一般的な教科書やプリントだけではなく、子供たち自身が関与し、楽しめるような活動を取り入れることで、学習体験が大きく向上しました。
具体的には、子供たちに自分で図形をデザインさせ、それが線対称かどうかを判断させる活動を行いました。
このような創造的なアプローチは、子供たちにとって新鮮であり、対称性に対する理解を深めるだけでなく、図形に対する興味も高めました。
さらに、アートや工作活動を組み合わせることで、線対称問題をより実践的で楽しいものに変えました。
例えば、子供たちに対称的な模様や図形を描かせたり、対称性をテーマにしたアートワークを作成させたりしました。
これらの活動は、数学的な概念を学ぶだけでなく、子供たちの創造的な表現力や芸術的なスキルも育てました。
創造性を促す教材の使用は、線対称問題への興味を持続させ、学習過程をよりエンゲージングで記憶に残るものにしました。
子供たちが自分自身の創造性を探求し、それを数学的な概念に適用することで、学習はより深い意味を持ち、効果的なものとなります。
線対称問題の勉強は、子供たちの空間認識能力、論理的思考力、そして創造性を育む重要なプロセスです。
この記事を通じて、私たちは線対称の概念の重要性、子供たちが直面する挑戦、およびそれらを克服するための効果的な勉強方法について詳しく見てきました。
個別化されたアプローチを取り、各子供の学習スタイルに合わせて教えること、視覚的ツールを活用して抽象的な概念を具体化すること、そして創造性を促す教材を用いることが、線対称問題の理解を深める鍵となります。
また、繰り返しを通じて、子供たちは線対称の概念をしっかりと身につけ、自信を持って問題に取り組むことができるようになります。
子供たちが線対称問題に取り組む過程は、単に算数のスキルを磨くだけでなく、論理的な思考や創造性を養う機会でもあります。
このような数学的概念を教えることは、子供たちの全体的な学習能力と成長に大きく貢献するため、親や教育者にとって非常に価値のある取り組みです。
線対称問題を通じて、子供たちは数学という科目を超えて、日常生活の中での多くの重要なスキルを学び取ることができます。



最後に、線対称問題のプリントを再度ご案内させていただきます!
反復練習にぜひ活用してください!
まずはサンプル
サンプルをご覧いただき、ご自宅で使えそうでしたら、ぜひダウンロードに進んでください。








簡単3ステップ:3枚無料プリントのダウンロード
お受験プリントの公式LINEアカウントを友だち追加いただいた方に、PDF版の無料プリントをプレゼントしています。



このブログを続けるモチベーションになりますので、ぜひ友だち追加をお願いします!


*写真は「回転図形」のサンプルです。


*パソコンでURLを開くと自動でダウンロード画面になります。
*PDF版の最後には「答え」がついてますが、無料プレゼントしている3枚以外の答えもついています。ご興味いただけましたら、以下のNoteもご覧ください*
ダウンロードエラーになってしまったら


無料プリントのURLがLINEアプリで開けないことがあります。
もしも「ページが開けません」というエラーになってしまったら、右下の「・」が3つ並んだボタンをクリックして「ブラウザで開く」をクリックしてください。
プリントを開くことができます。

















