小学校受験は、子供たちにとっても親にとっても大きな挑戦です。
特に、問題解決能力を試すペーパーテストは、多岐にわたる知識とスキルが求められます。
この記事では、小学校受験のペーパーテストでよく出る6つの大項目（図形、数、推理、規則、言葉、常識）について、その解き方や対策を詳しく解説します。
各項目には、我が家で二人の子供がご縁をいただいた経験を踏まえて、子供が苦労するポイントや教え方のポイントも紹介しています。
この記事が一人でも多くのお子さんやご家族のお役に立てれば幸いです。
X (旧ツイッター)では、毎日3問、基礎力アップにつながるクイズを配信しています [フォローはコチラから]
インスタグラムではサクッとペーパー対策ができる動画を配信しています [フォローはコチラから]
＊お教室や市販の問題集の補助としてご利用いただくために低価格でのご案内ですが、内容は基礎から応用まで幅広く網羅しております＊
【基礎・応用】頻出科目の基礎、応用を幅広く理解度確認したい方向け
【基礎・応用】回転図形、サイコロ、鏡など図形問題の理解度確認したい方向け
【基礎・応用】シーソー、魔法の箱、ルーレットなど条件推理問題の理解度確認したい方向け
【基礎・応用】計数、数の分割・構成など数の問題の理解度確認したい方向け
図形問題は、小学校受験の中でも特に重要な項目の一つです。これらの問題は、子供たちの視覚的な理解力や空間認識能力を試すもので、基本的な図形の認識から図形の組み合わせ、変形、移動、回転といった複雑な問題まで幅広く出題されます。
ここでは、それぞれの小項目について詳しく解説します。
子供たちはまず、基本的な図形を認識することから始めます。これには、四角形や三角形、円などのシンプルな図形だけでなく、五角形や六角形といった多角形も含まれます。また、これらの図形を描写する能力も問われます。子供が苦労するポイントは、図形の特徴を正確に理解し、それを紙上に再現することです。例えば、正方形と長方形の違いを理解し、それぞれを正確に描くことが求められます。教え方のポイントは、各図形の特徴を視覚的に示しながら教えることで、子供たちが図形の形状や特性を理解しやすくすることです。具体的な図形を用いて、図形の名前と特徴を一緒に覚えることが効果的です。さらに、子供たちは図形の面積や周囲の長さといった概念も学びます。これらの概念は、図形の大きさや形状を理解するために重要です。また、図形の対称性や回転による形状の変化といった概念も紹介します。これらの概念を理解することで、子供たちは図形の特性をより深く理解することができます。
次に、複数の図形を組み合わせて新たな図形を作る問題や、図形が重なった場合の形状を理解する問題が出題されます。これらの問題は、子供たちの空間認識能力や論理的思考力を試すものです。子供が苦労するポイントは、複数の図形が組み合わさった複雑な形状を理解し、それを分解することです。例えば、二つの円が重なった場合、その重なった部分の形状を理解することが求められます。教え方のポイントは、具体的な図形を用いて、図形の組み合わせや重ね合わせの概念を視覚的に示すことです。具体的な図形を用いて、図形の組み合わせや重ね合わせの概念を視覚的に示し、それを基に推理する練習を重ねることが効果的です。また、子供たちは図形の組み合わせによって新たな図形が作られる概念を学びます。例えば、二つの三角形が組み合わさって四角形になるといった具体的な例を通じて、図形の組み合わせの概念を理解します。さらに、図形が重なった場合の形状を理解するためには、図形の部分的な視覚化が必要となります。これにより、子供たちは図形の部分と全体の関係を理解することができます。
さらに、図形が変形したり、移動したり、回転したりした場合の形状を予測する問題も出題されます。これらの問題は、子供たちの空間認識能力を一層試すもので、図形の性質を理解し、それを基に推理する能力が求められます。子供が苦労するポイントは、図形が変形や移動、回転をした後の形状を正確に予測することです。例えば、正方形が45度回転した後の形状を理解することが求められます。教え方のポイントは、具体的な図形を用いて、図形の変形や移動、回転の概念を視覚的に示し、それを基に推理する練習を重ねることです。具体的な図形を用いて、図形の変形や移動、回転の概念を視覚的に示し、それを基に推理する練習を重ねることが効果的です。また、図形の変形や移動、回転を通じて、子供たちは図形の性質が変わらないという不変性の概念を学びます。これにより、子供たちは図形の本質的な特性を理解することができます。
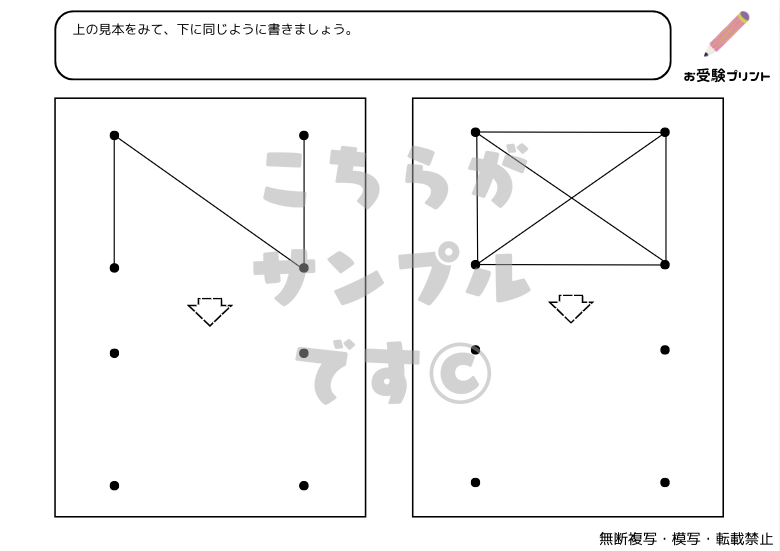
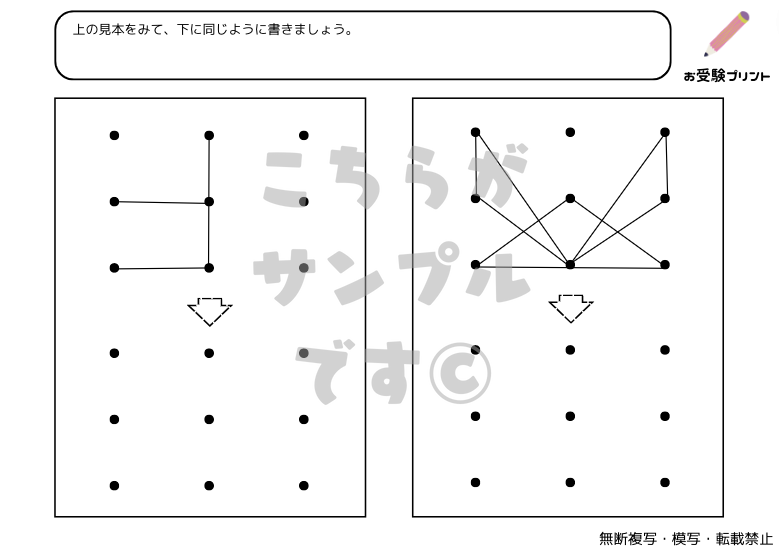
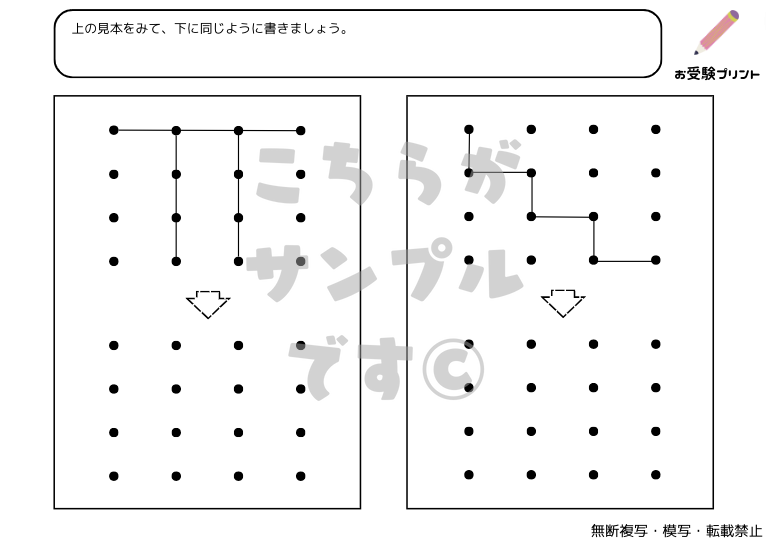
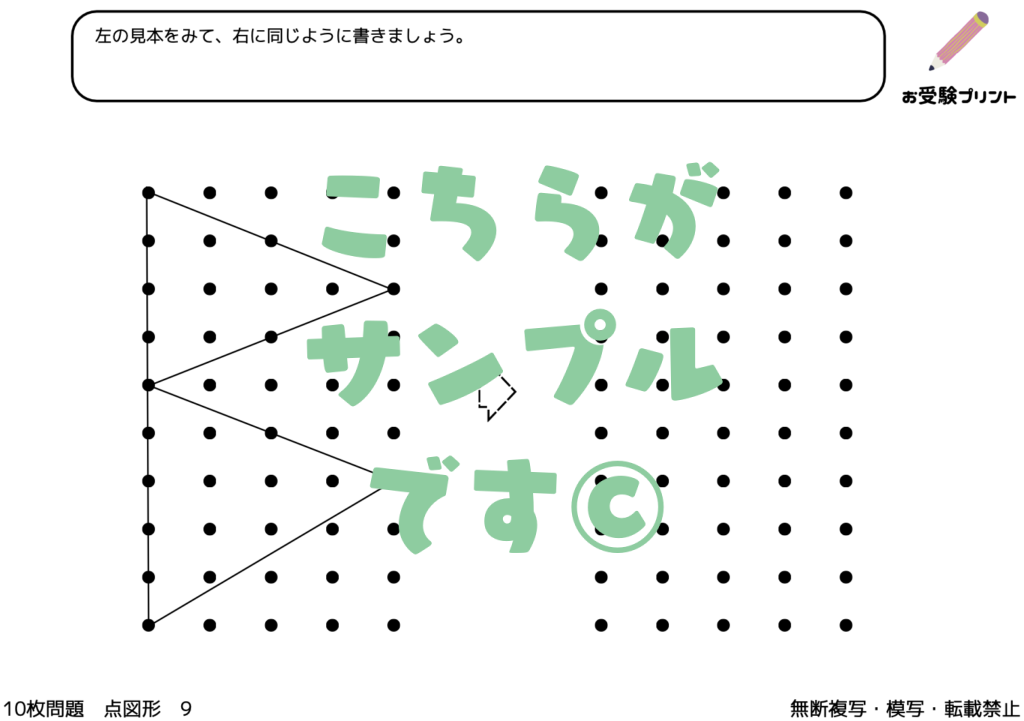
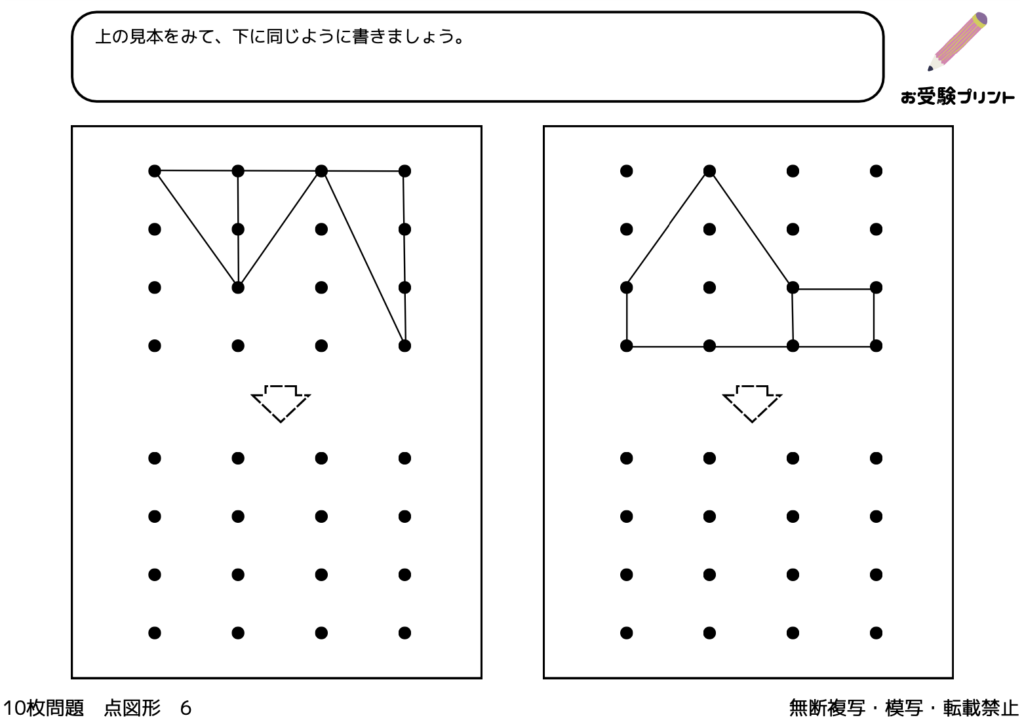
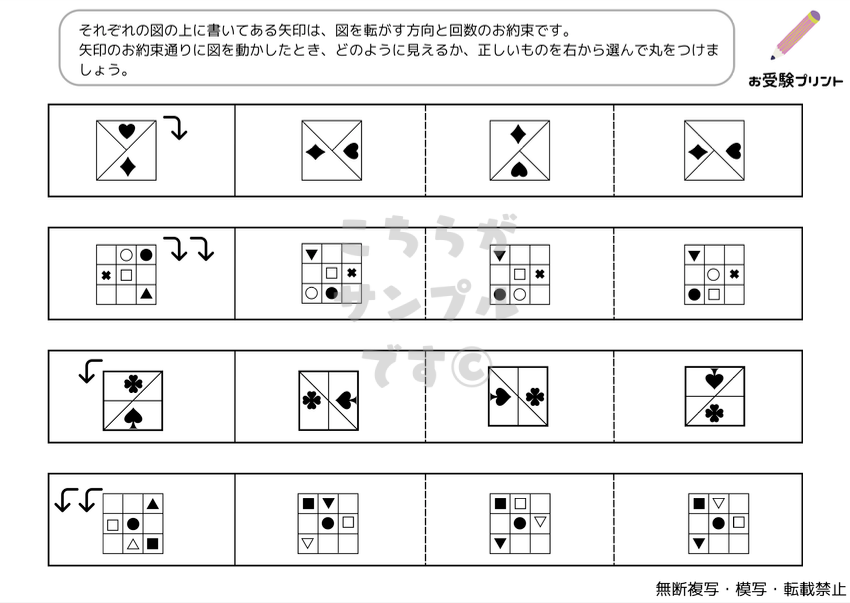
「点図形問題」は、小学校受験の一部としてよく出題される問題です。この問題は、点が描かれた図形を観察し、そのパターンや形状を理解することを求められます。特に、同形、左右対称、矢印などの観点から問題が出題されます。
例えば、同形編では、与えられた点図形が同じ形状をしているかどうかを判断する問題が出ます。一方、左右対称編では、点図形が左右対称であるかどうかを見極める問題が出題されます。また、矢印編では、点図形が示す方向を理解し、そのパターンを読み取る問題が出ます。
これらの問題は、子供たちの視覚的な理解力や空間認識能力を鍛えるのに役立ちます。また、論理的思考や問題解決能力も同時に育てることができます。
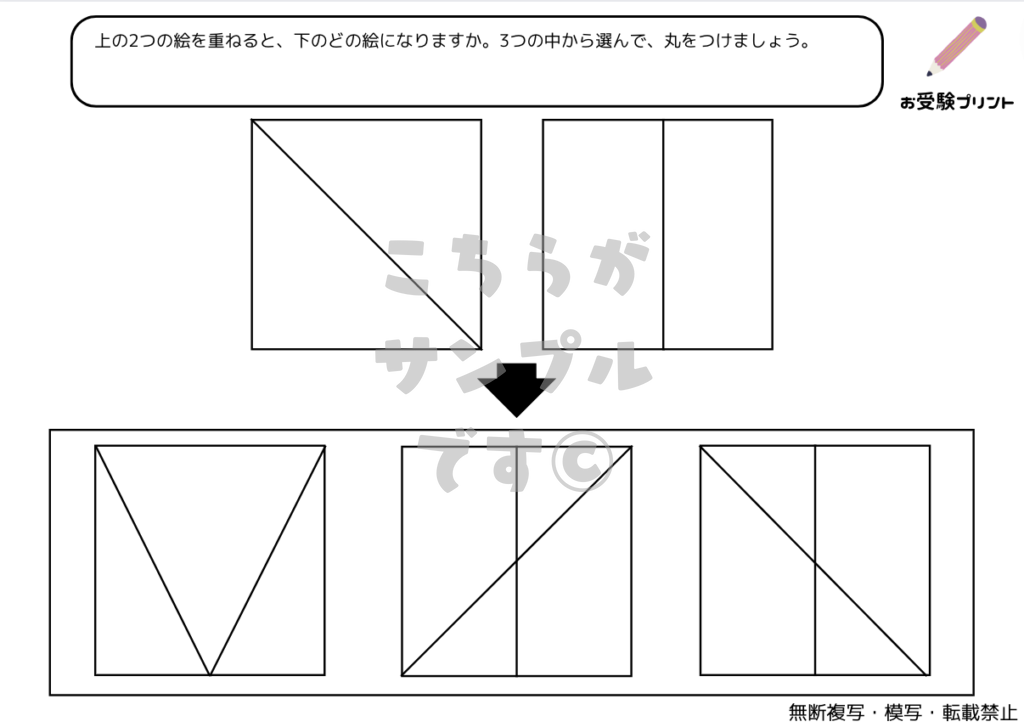
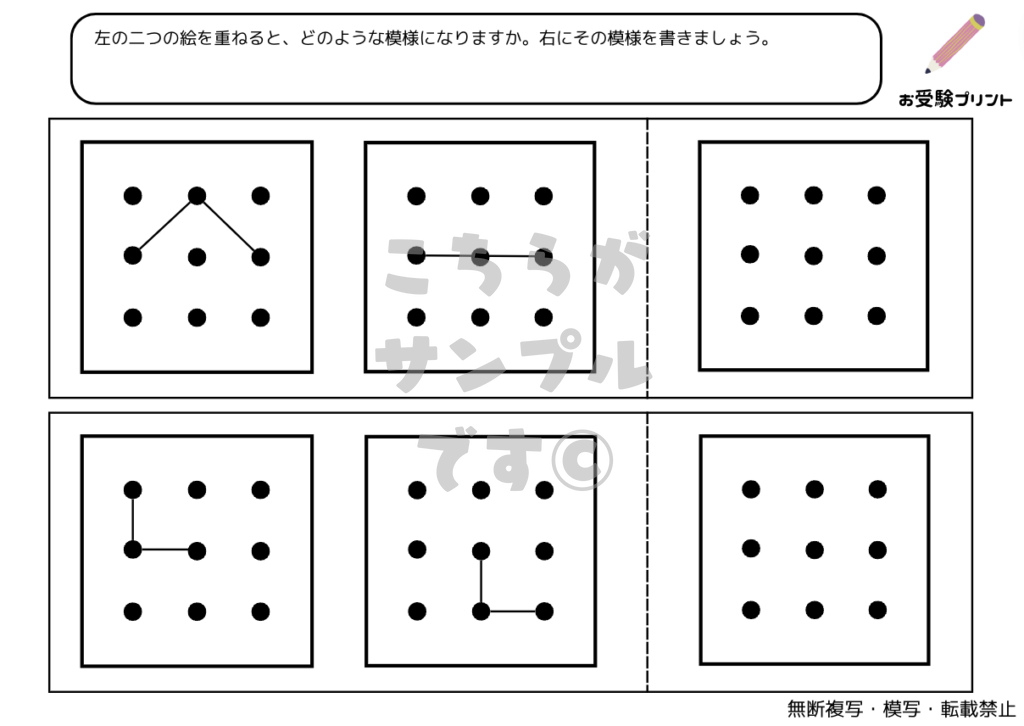
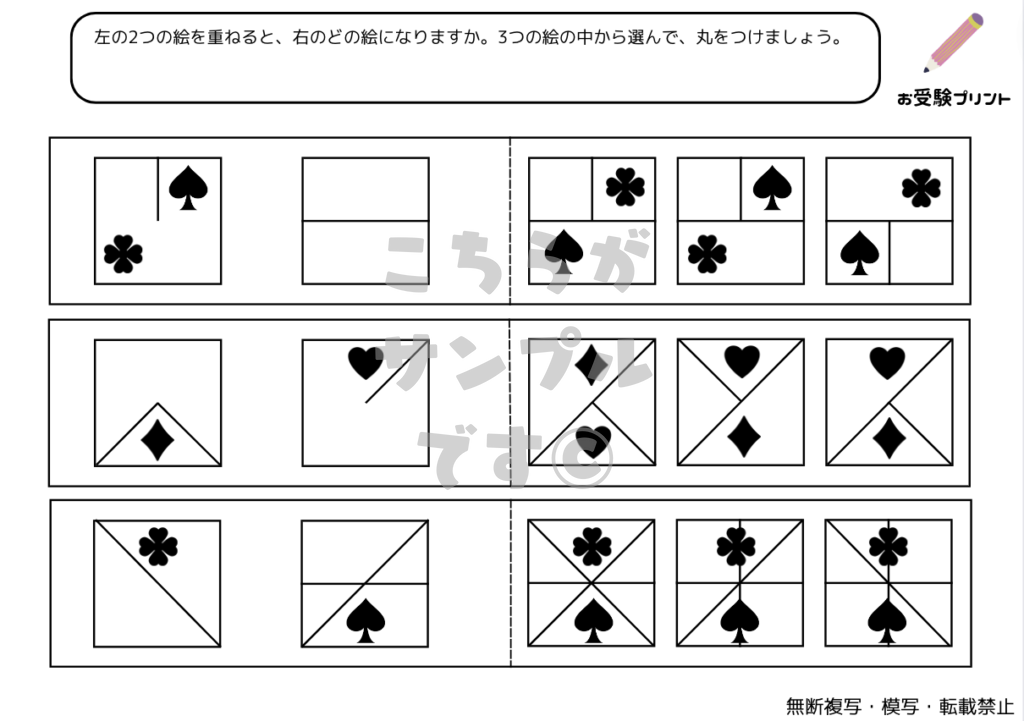
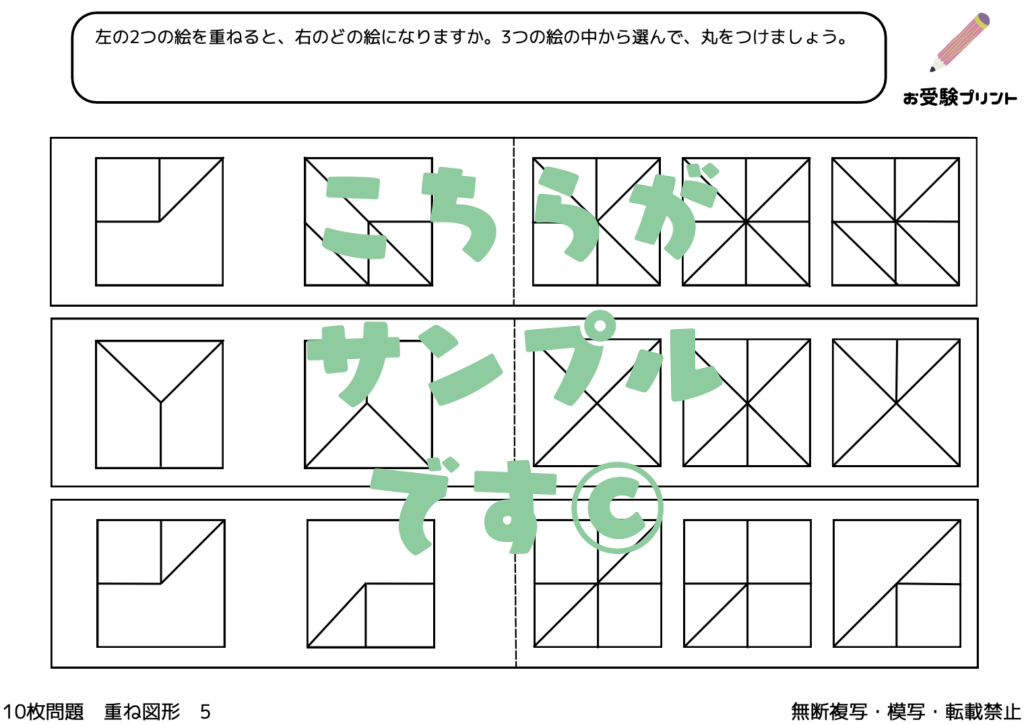
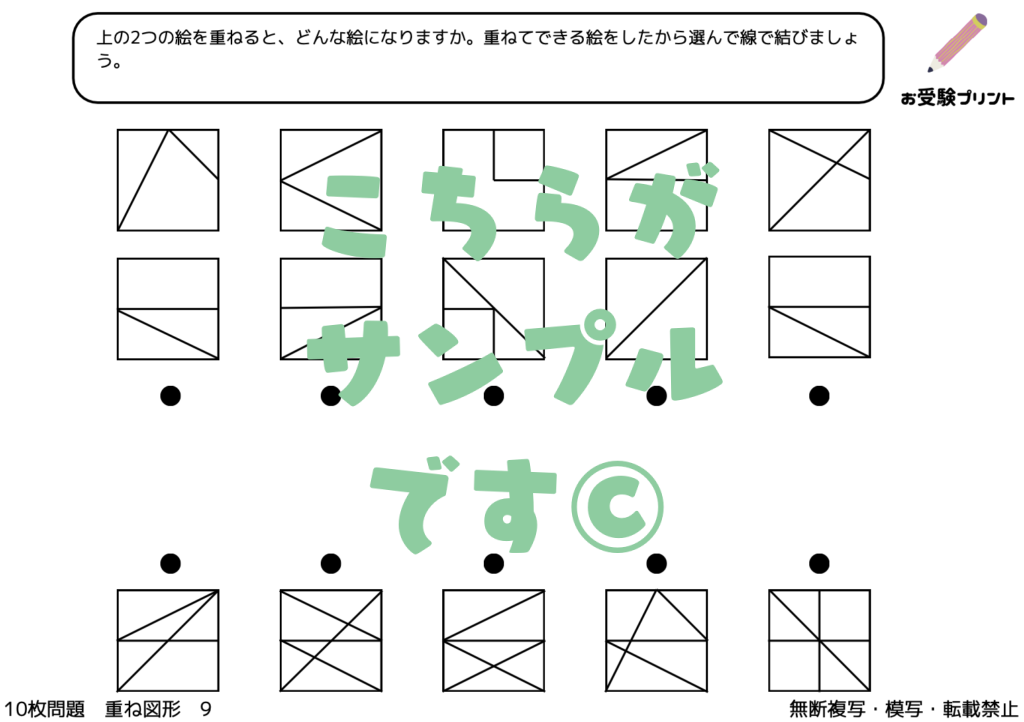
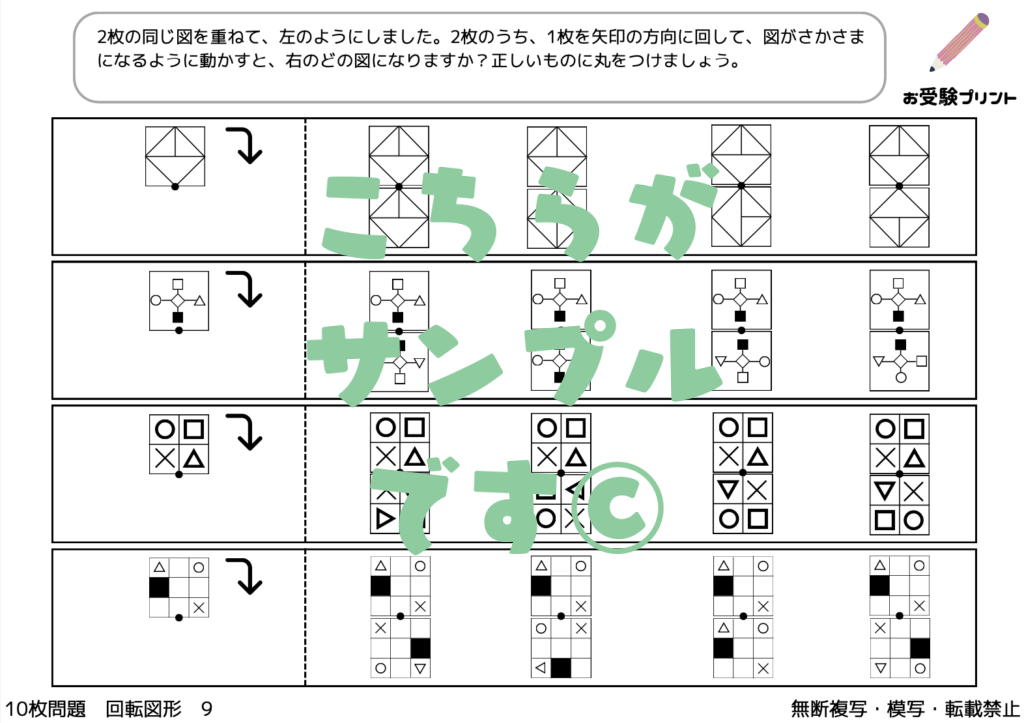
「重ね図形問題」は、複数の図形が重ね合わされた状態を想像し、その結果どのような図形が出来上がるかを予測する力を試すものです。具体的には、2枚や3枚の図形を重ねた場合、または図形が対称に重ねられた場合など、さまざまなパターンが考えられます。また、「ふたをする編」のように、一部が覆われて見えない部分を推測する問題もあります。
この問題を解くためには、空間認識能力と論理的思考が必要となります。子供たちは、図形の形状や配置を理解し、それらがどのように組み合わさるかを想像することで、問題の答えを導き出します。このスキルは、日常生活や他の学習領域でも役立つため、小学校受験の準備として「重ね図形問題」の練習を行うことは非常に有益です。
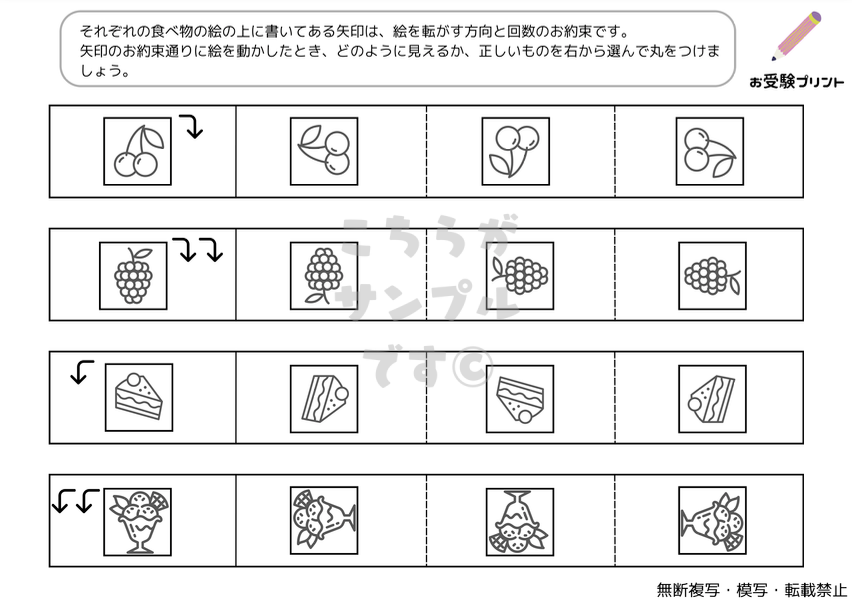
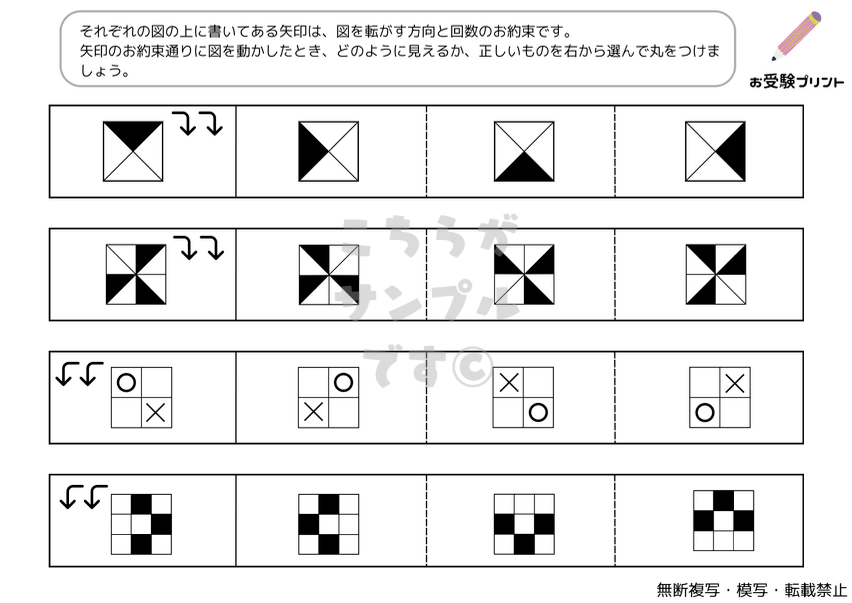
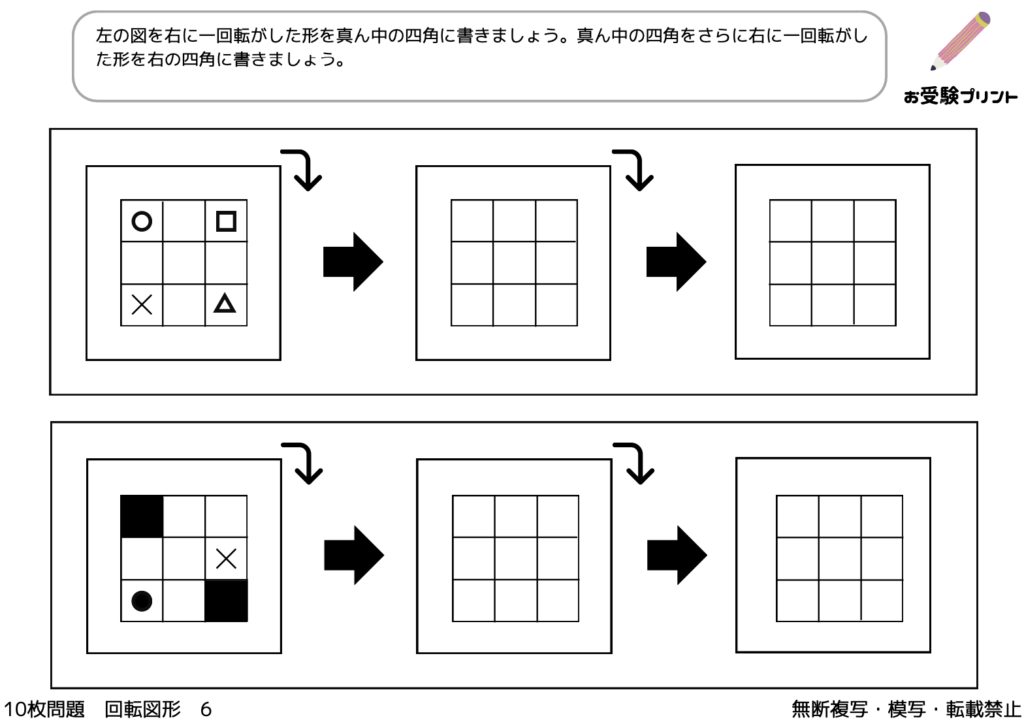
「回転図形問題」は、図形が一定の角度で回転した後の姿を予想する問題で、空間認識能力と論理的思考力を鍛えるのに役立ちます。
図形が90度、180度、270度など特定の角度で回転した後の姿を予想する問題で、子供たちが空間認識能力を鍛えるのに役立ちます。また、子供たちは図形が回転した後の位置や向きを理解し、それを基に問題を解く能力を身につけることが求められます。
一回転図形問題は子供たちの空間認識能力と論理的思考力を鍛えるのに非常に有効な問題であると言えます。これらの能力は、小学校受験だけでなく、日常生活や他の学問領域でも役立つため、しっかりと理解し、練習することが重要です。
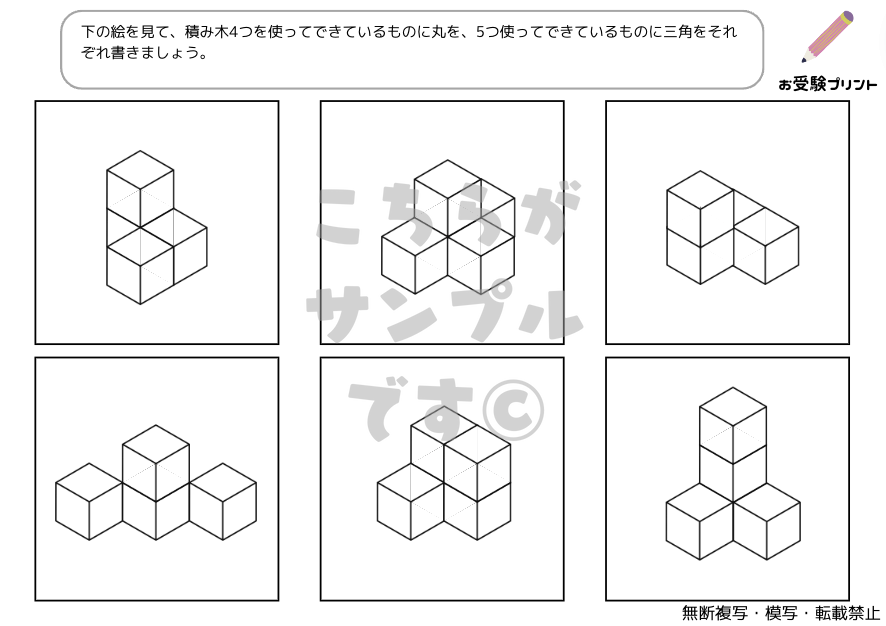
「立体図形問題」は、子供たちが立体的な視点を持つことを助け、空間認識能力を育てるためのものです。具体的には、図形の移動や回転、図形の変化、図形推理などが含まれます。
例えば、図形の回転問題では、特定の角度で回転した後の図形を予測する能力が問われます。また、図形推理問題では、一連の図形のパターンを理解し、次に来る図形を推測する能力が求められます。
これらの問題は、子供たちが視覚的な情報を解釈し、複雑な問題を解決するための基礎となるスキルを育てます。また、これらの問題を解くことで、子供たちは論理的思考や問題解決能力を鍛えることができます。
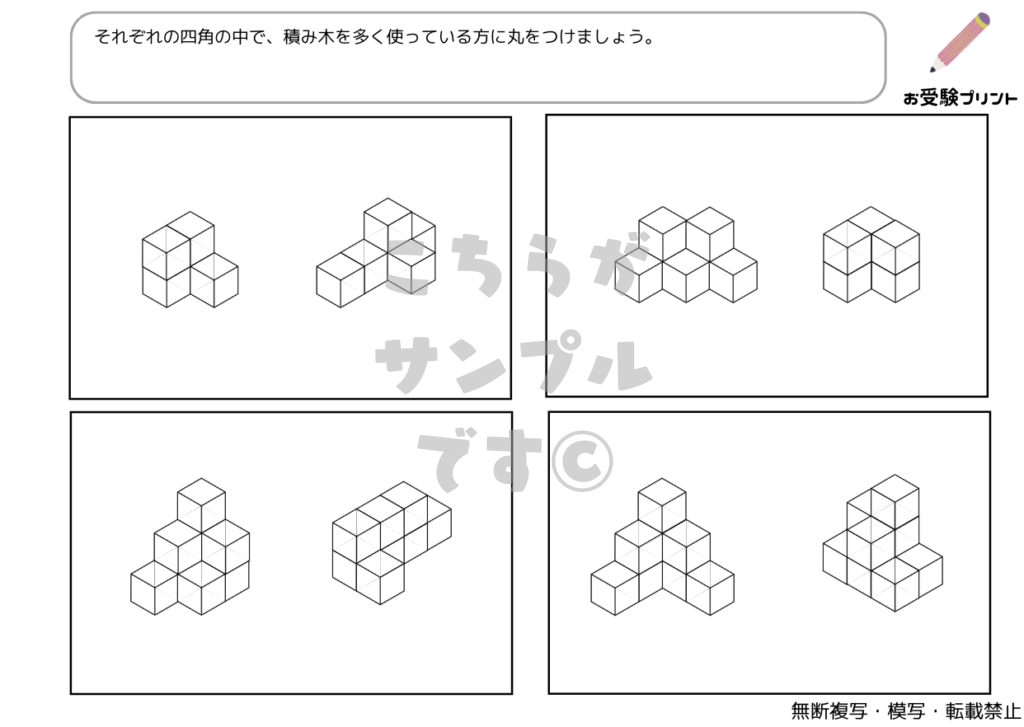
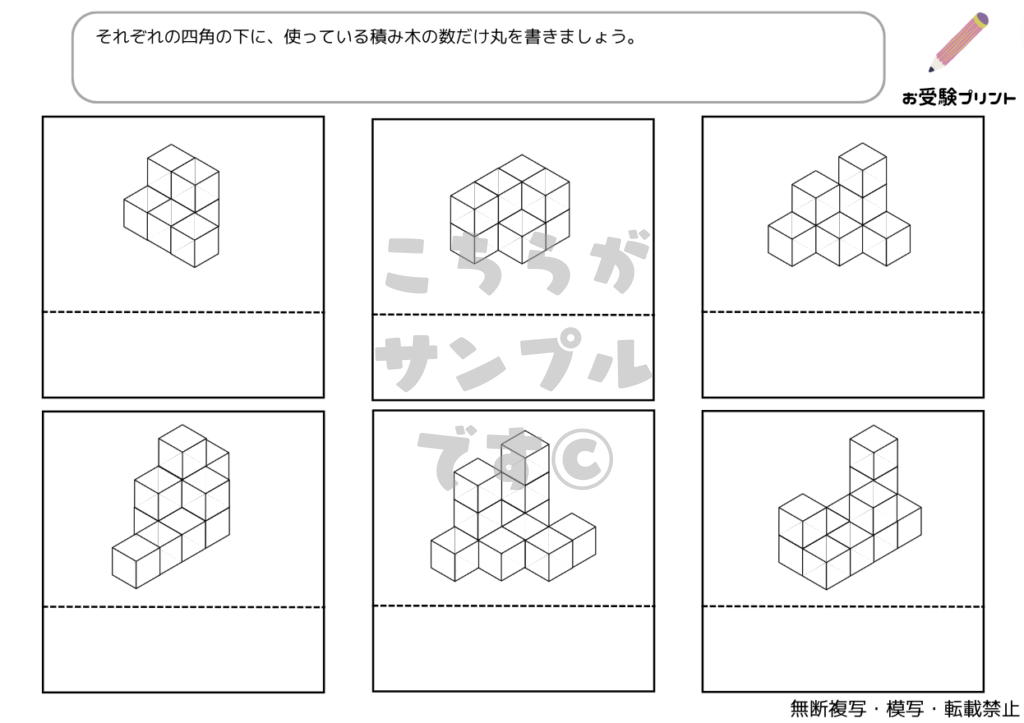
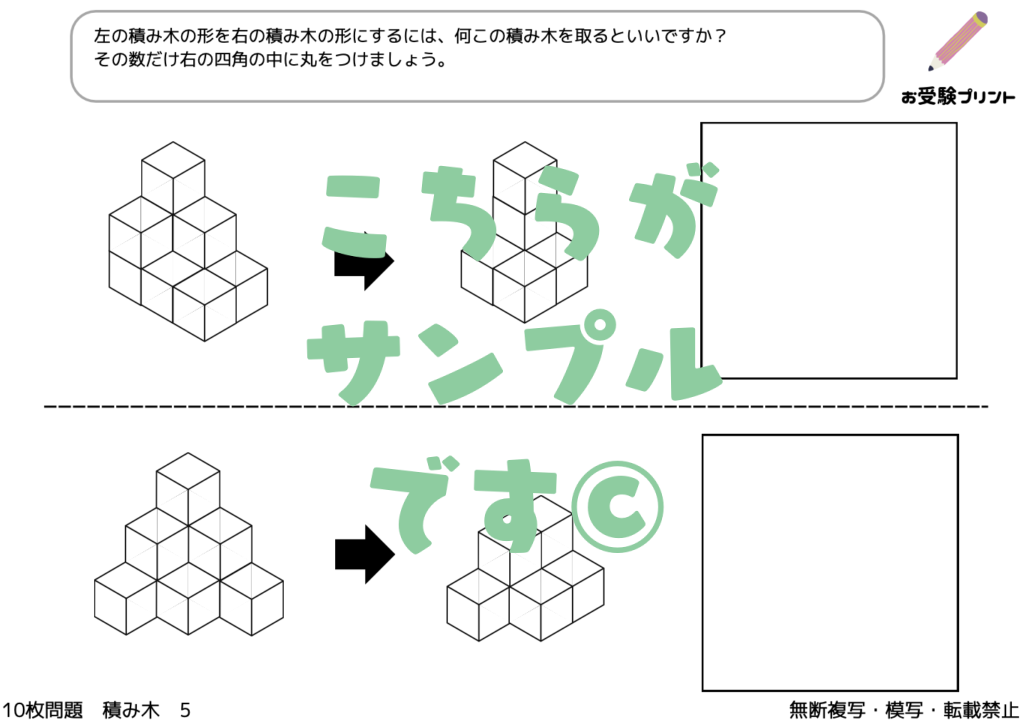
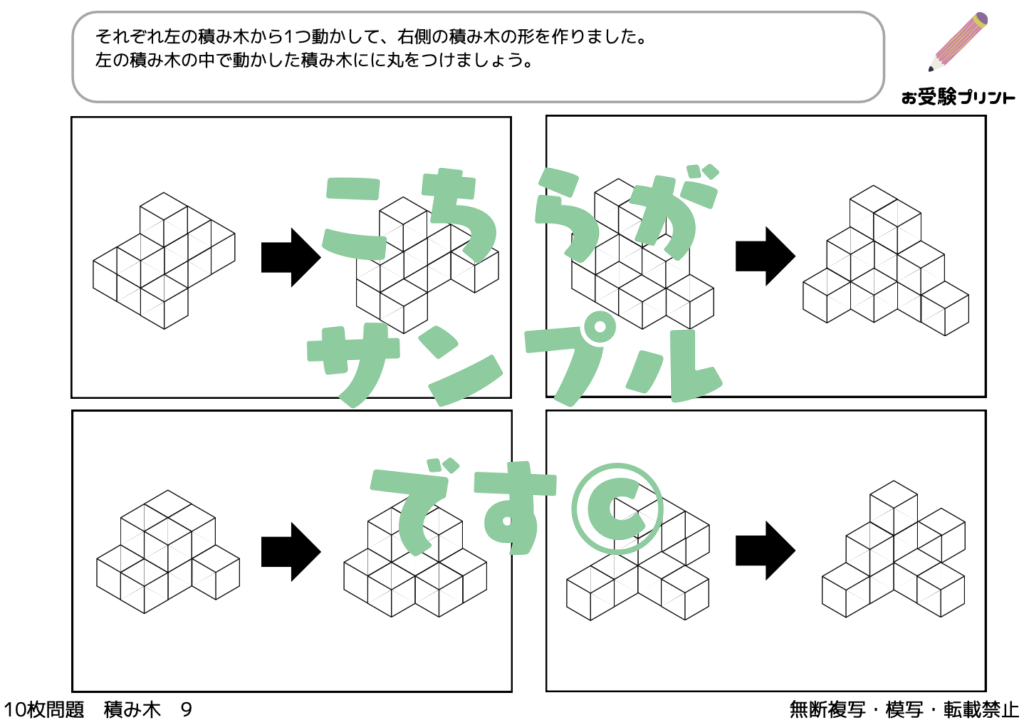
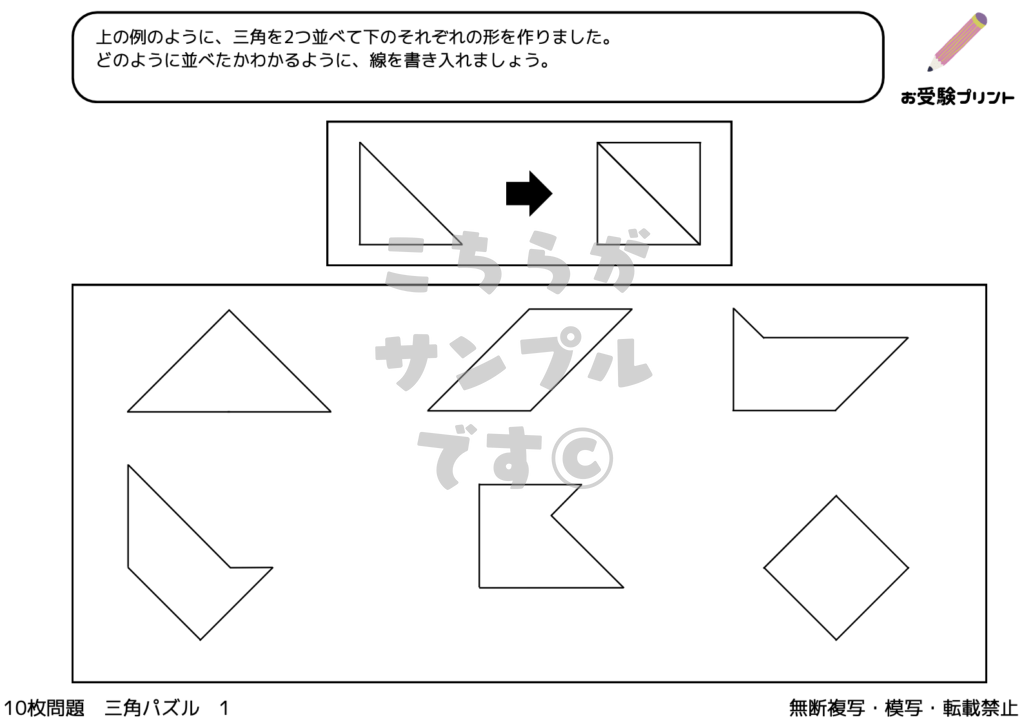
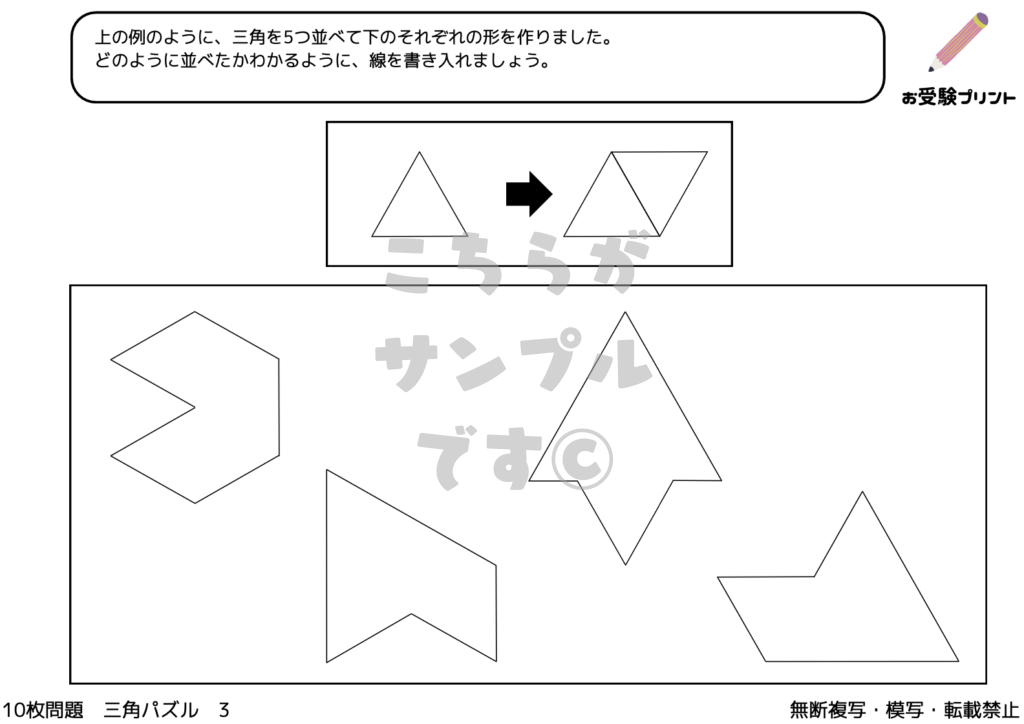
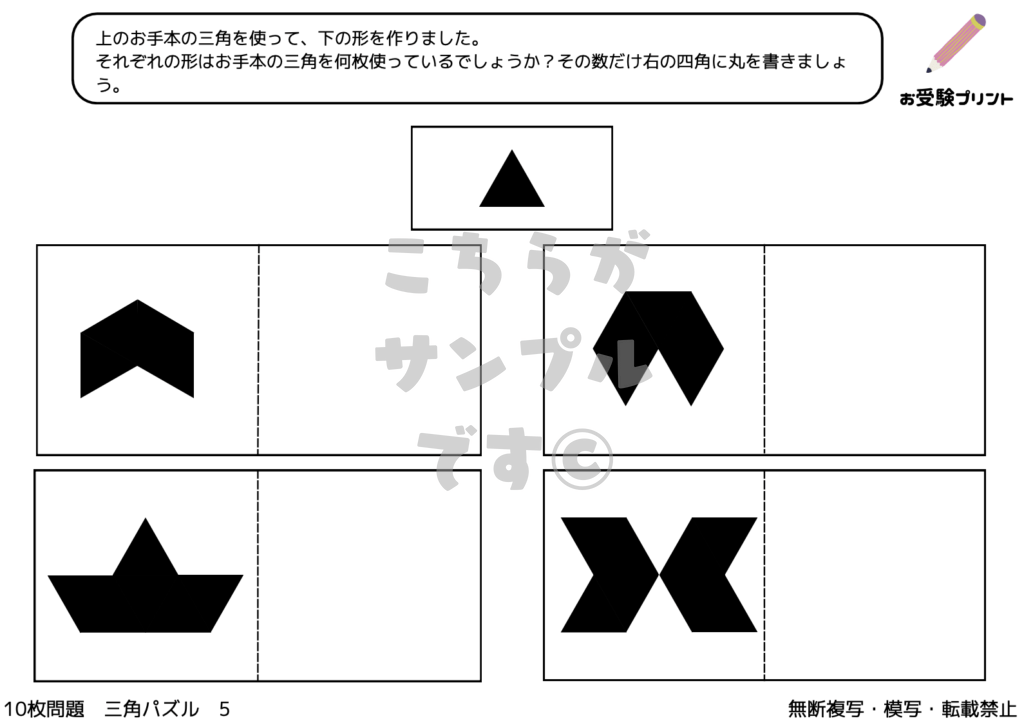
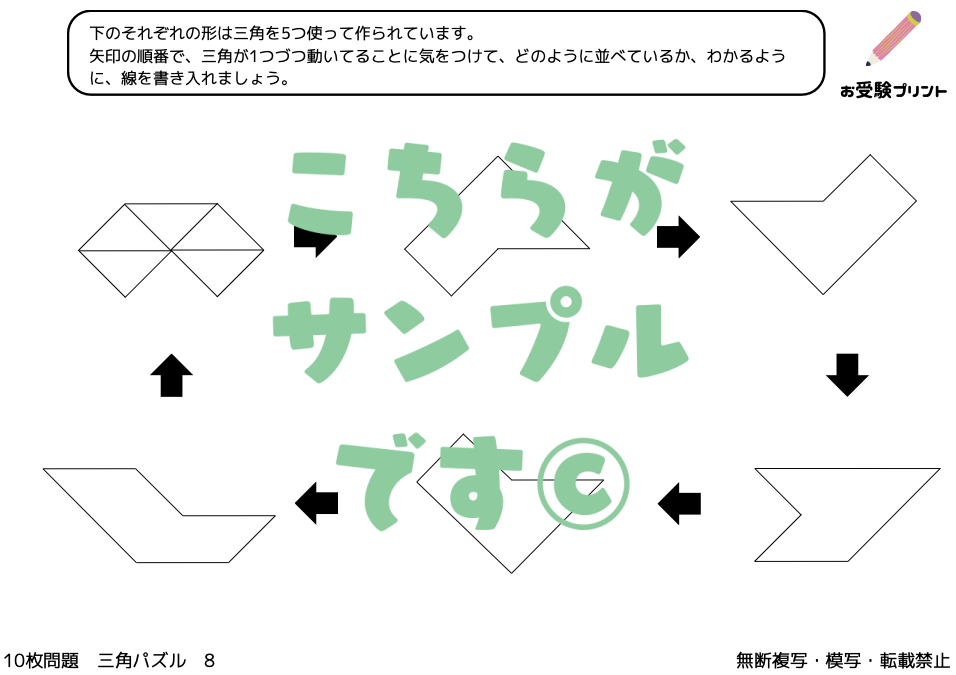
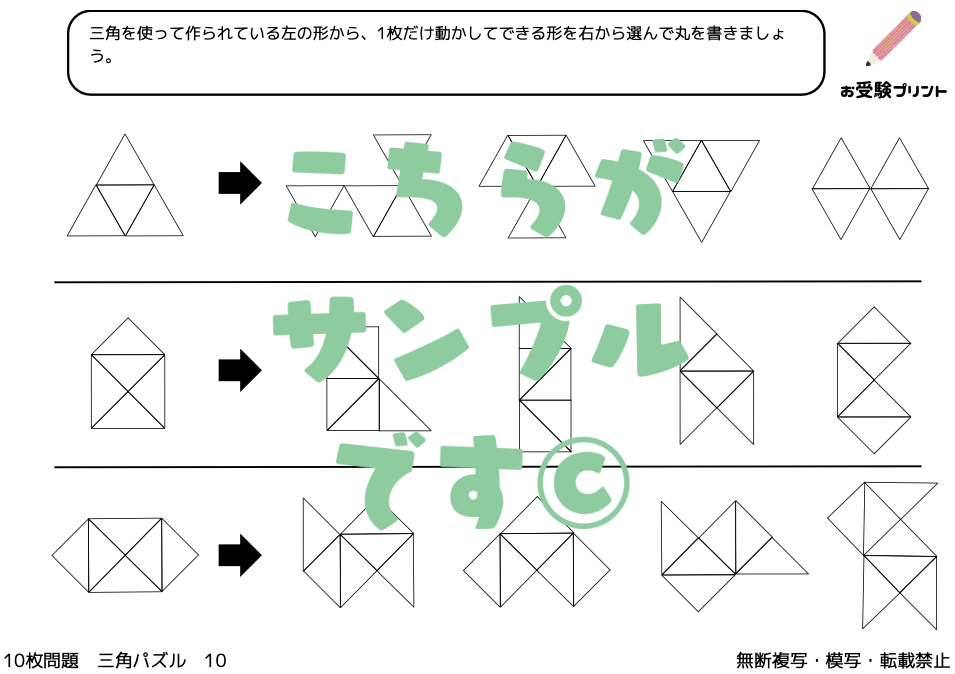
「三角パズル問題」とは、図形の理解と空間認識能力を試す問題です。この問題では、いくつかの三角形のピースを使って、指定された形を作り出す課題が出されます。子供たちは、与えられたピースをどのように組み合わせれば目的の形が完成するのかを考えなければなりません。
このプロセスでは、ピースの形状を認識し、それらがどのように連動して全体の形を作るかを理解する必要があります。三角パズル問題は、ただ形を合わせるだけではなく、論理的思考、問題解決能力、そして創造性を養うための絶好の機会をとなります。
このような問題に取り組むことで、子供たちは形と空間に対する直感的な理解を深め、数学的な概念を自然と身につけることができます。
「図形構成問題」とは、与えられた図形を組み合わせて新たな図形を作り出す問題です。これは子供たちの空間認識能力や論理的思考力を鍛えるのに非常に有効です。例えば、特定の形状のブロックを組み合わせて、指定された形状を作り出すといった問題があります。
一方、「図形の分割問題」は、与えられた図形を特定の数や形に分割する問題です。これは子供たちの数理的思考力や問題解決能力を鍛えるのに役立ちます。例えば、正方形を4つの同じ大きさの正方形に分割するといった問題があります。
これらの問題は、小学校受験の際に出題されることが多く、子供たちが学校で学ぶ数学の基礎を形成する重要な部分です。
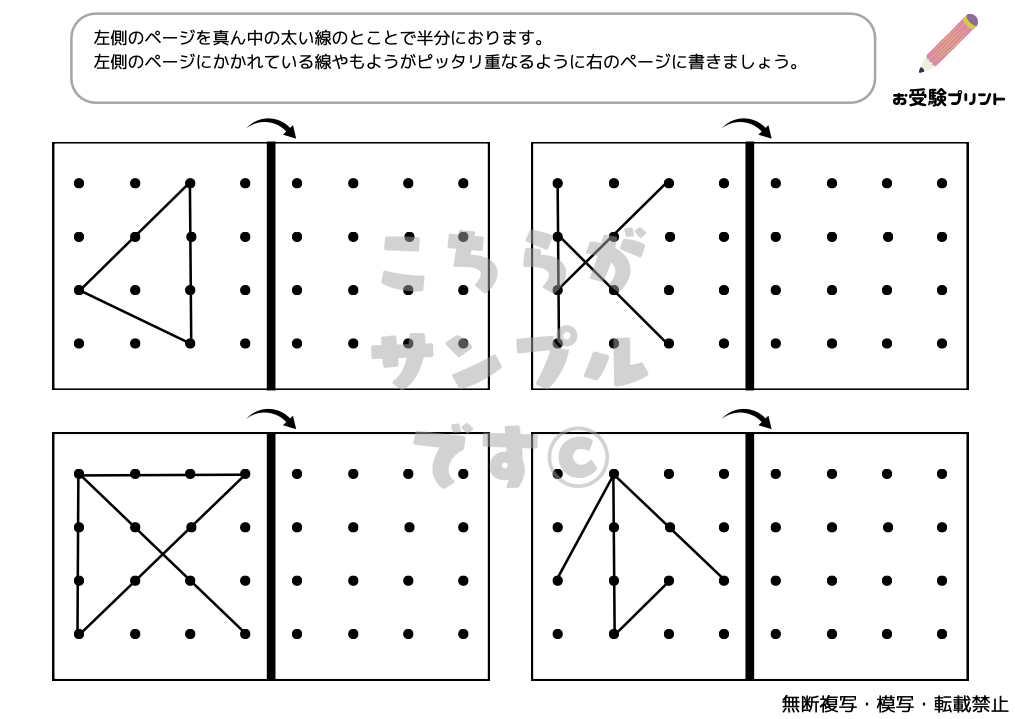
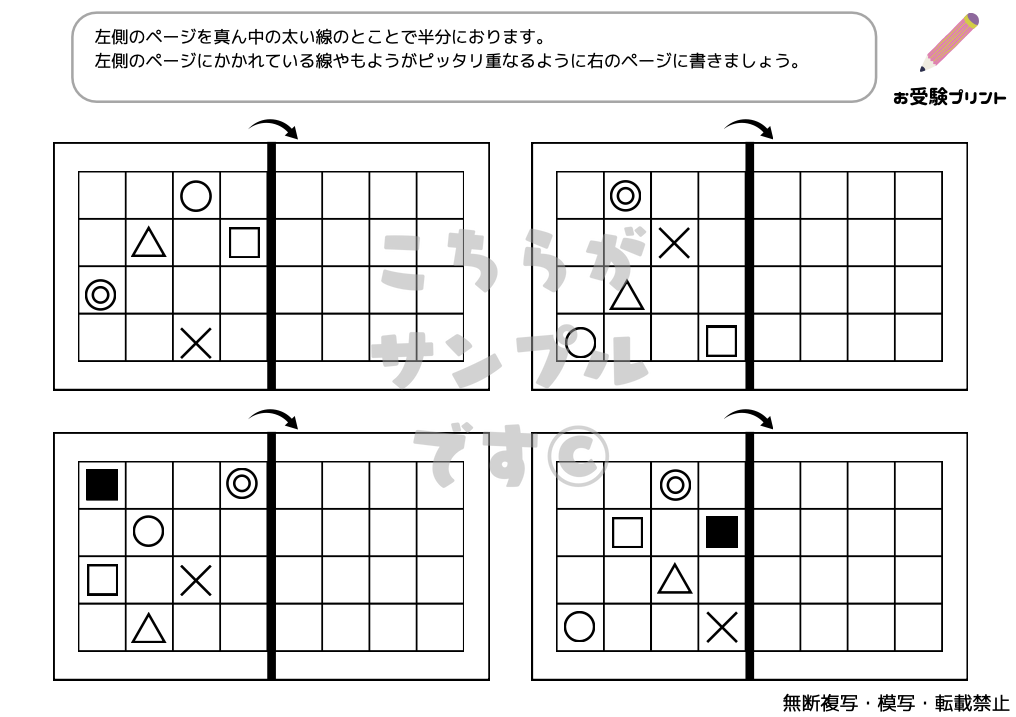
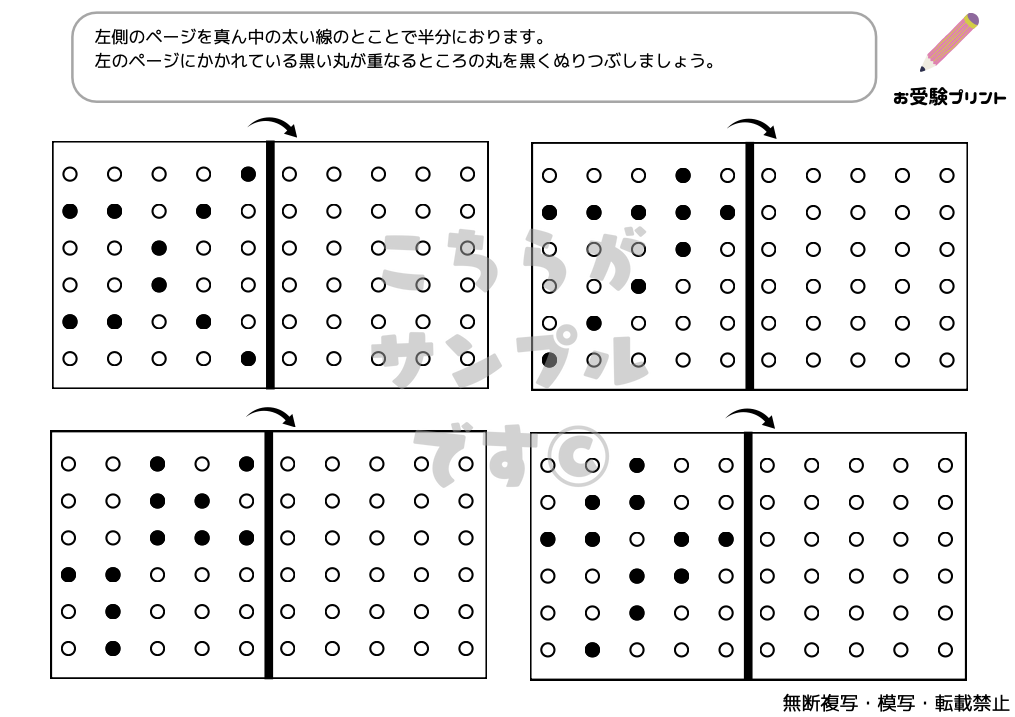
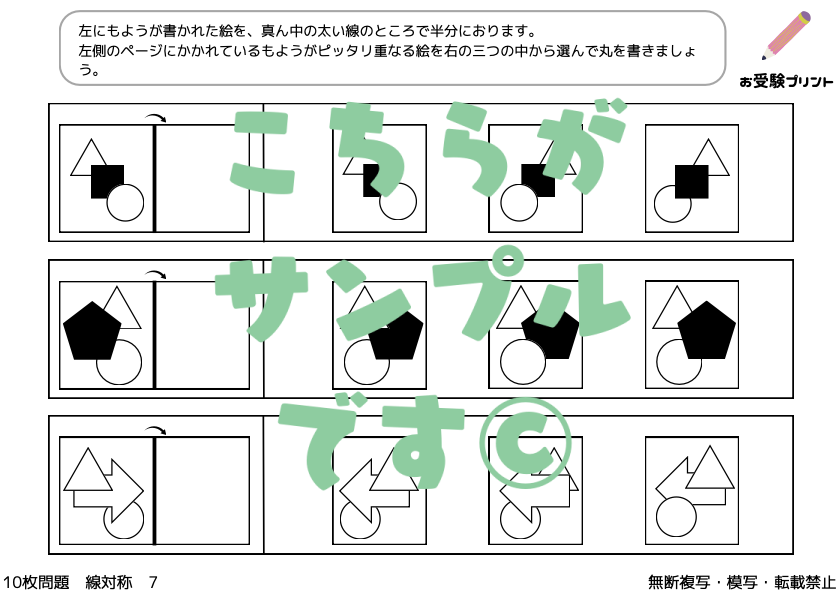
「線対称問題」とは、ある直線（対称軸）を中心にして、図形が左右または上下に完全に重なるように描かれているかを判断する問題です。この種の問題は、子供たちにとって、形や空間に関する深い理解を必要とします。線対称問題では、特定の図形が与えられ、その図形が指定された対称軸に関して線対称かどうかを判断しなければなりません。
また、与えられた図形の対称軸を見つけることや、対称軸に沿って新しい図形を作成する問題も出題されます。これらの問題は、幾何学的な知識だけでなく、視覚的な分析能力も養います。子供たちは図形を観察し、そのパターンや構造を理解することで、答えに近づくことができます。
このような問題は、子供たちの思考力、問題解決能力、そして創造性を育むのに非常に役立ちます。
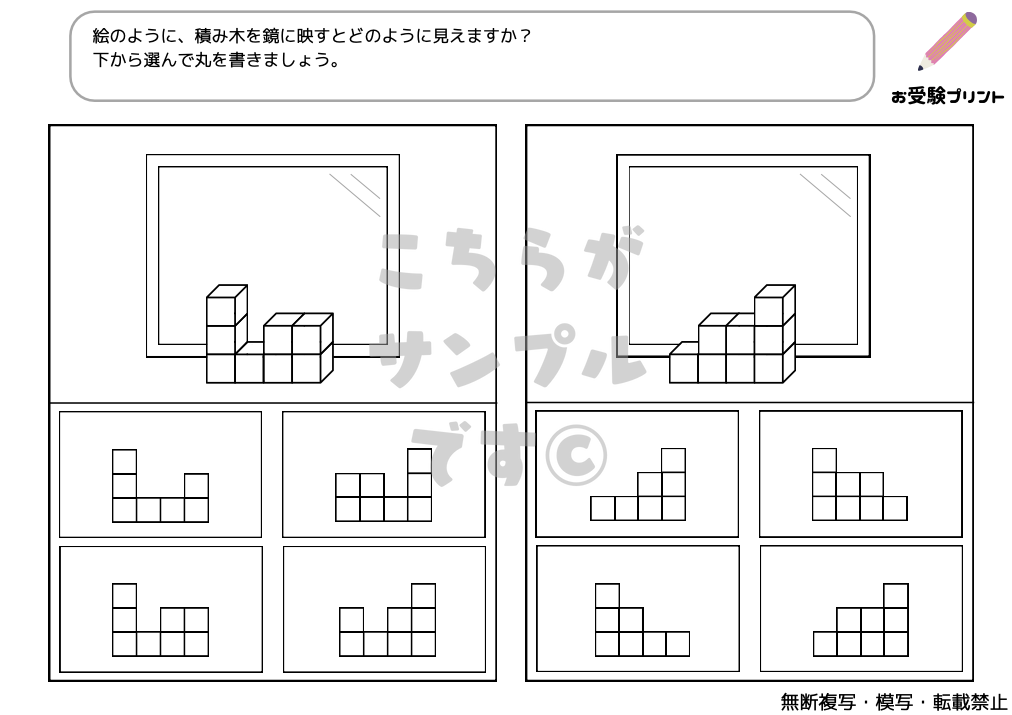
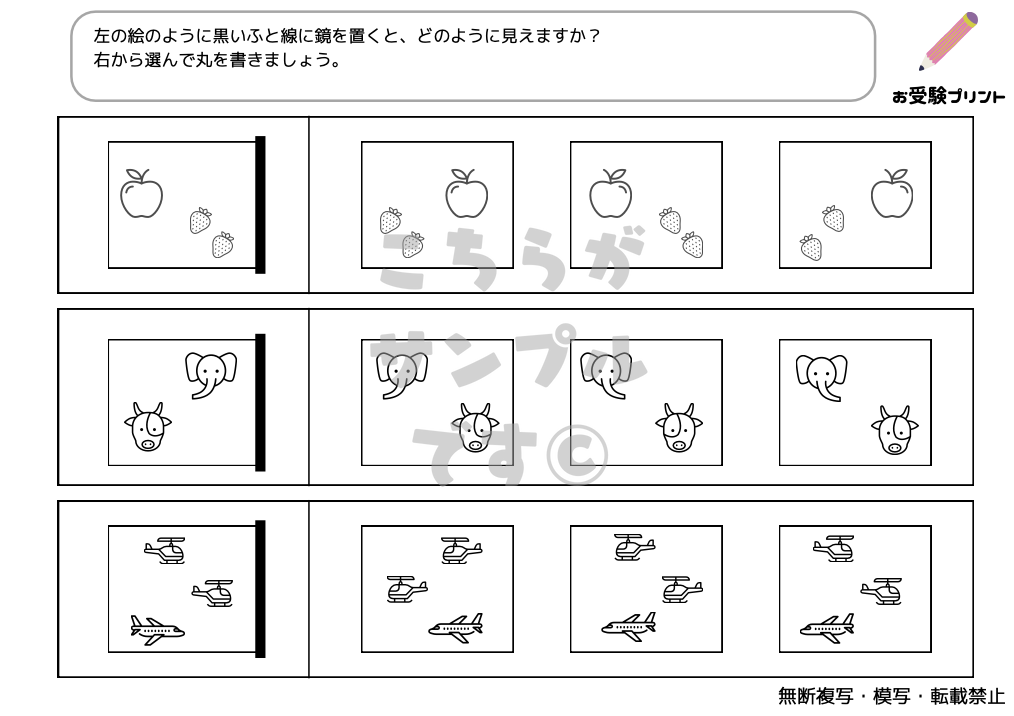
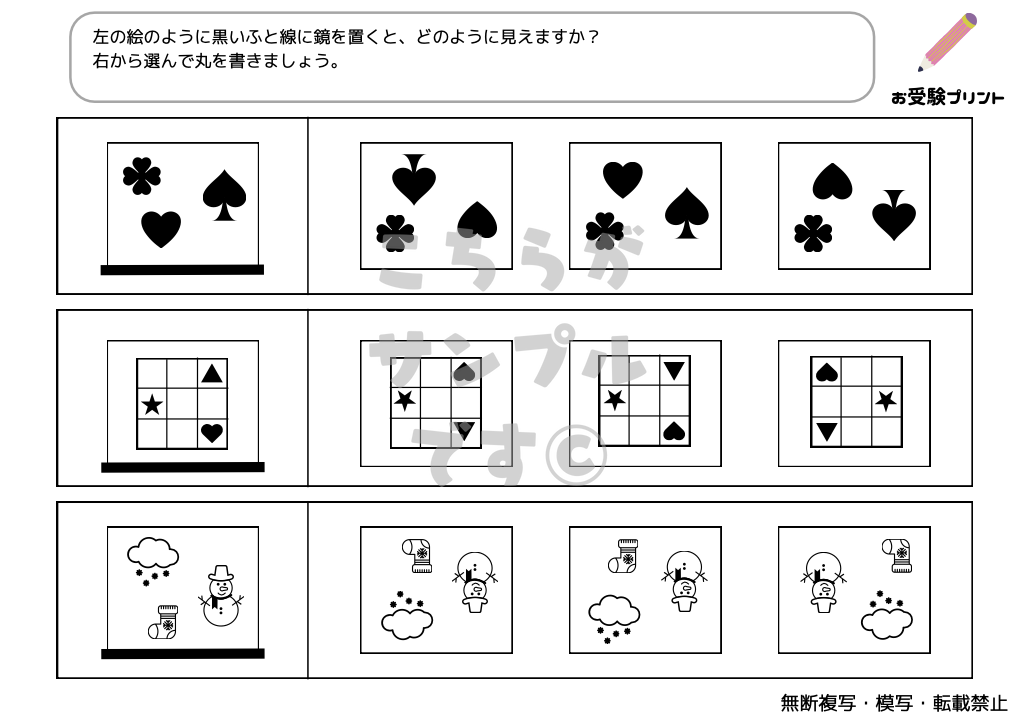
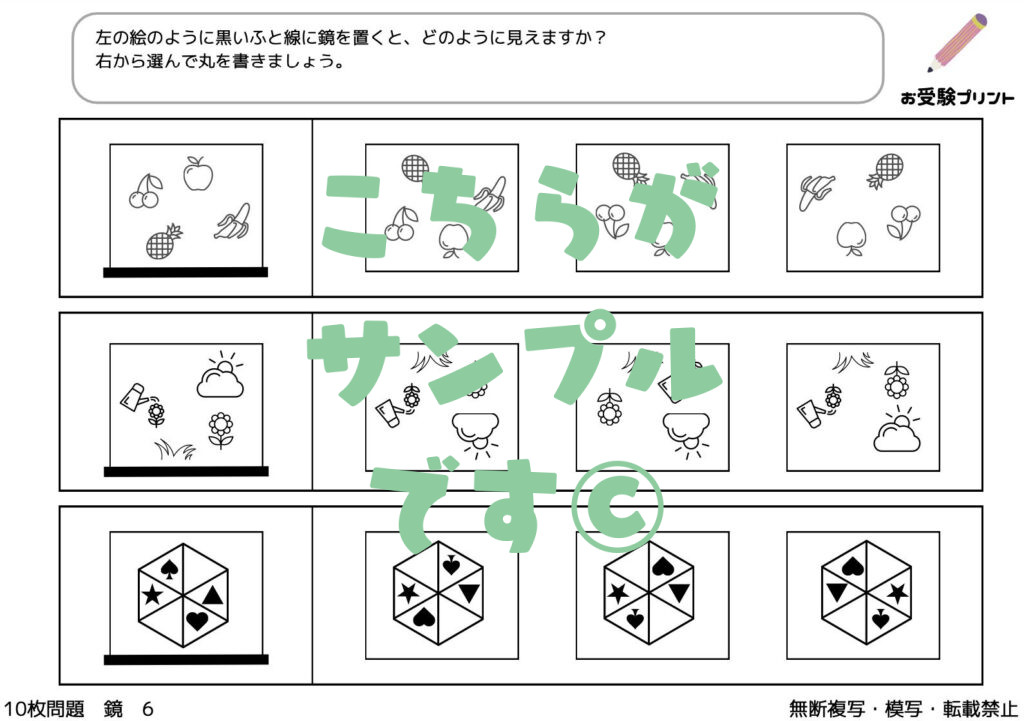
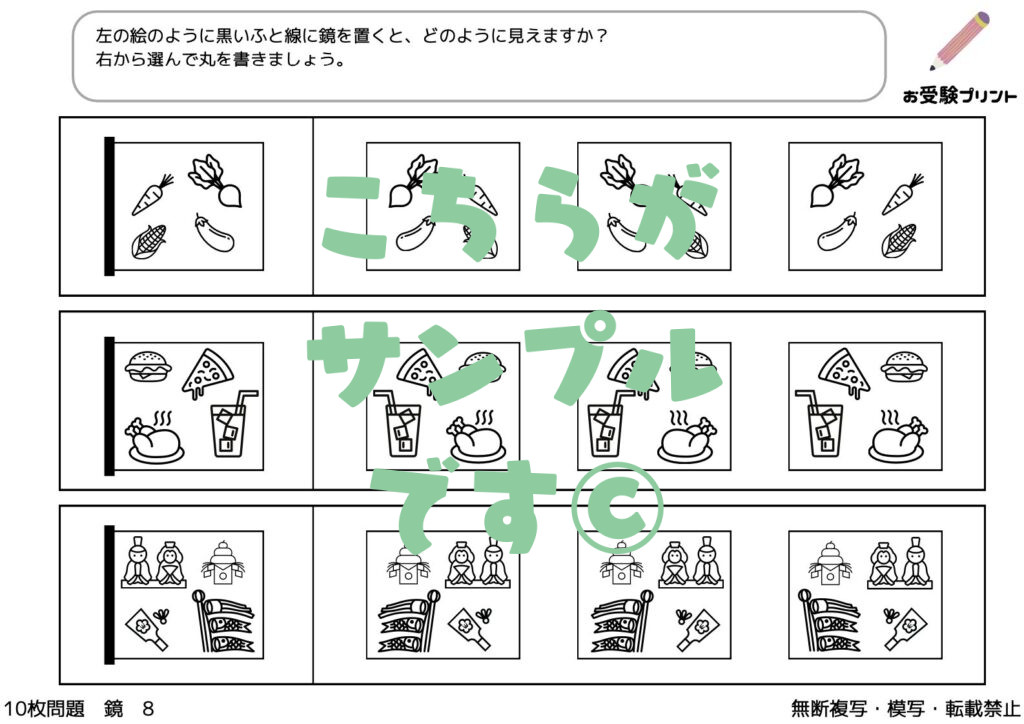
「鏡問題」とは、子供たちが鏡を通して物体や図形がどのように映るかを理解し、答える問題です。具体的には、物体や図形が鏡に映ると、左右が反転するという特性を基に、どのように映るかを予測する力を養います。
この問題は、小学校受験において子供たちの空間認識能力を試すためによく用いられます。
たとえば、特定の形の物体を鏡の前に置いた時、その鏡映像がどのように見えるかを考えさせるのです。
これには、上下は変わらず、左右が逆になるという基本的な鏡の性質を理解することが必要です。また、この問題を解くことは、子供たちの観察力や論理的思考力を養うのにも役立ちます。
視覚的な情報をもとに、抽象的な考えを形成し、その結果を言葉や絵で表現することは、知的成長にとって重要なステップです。
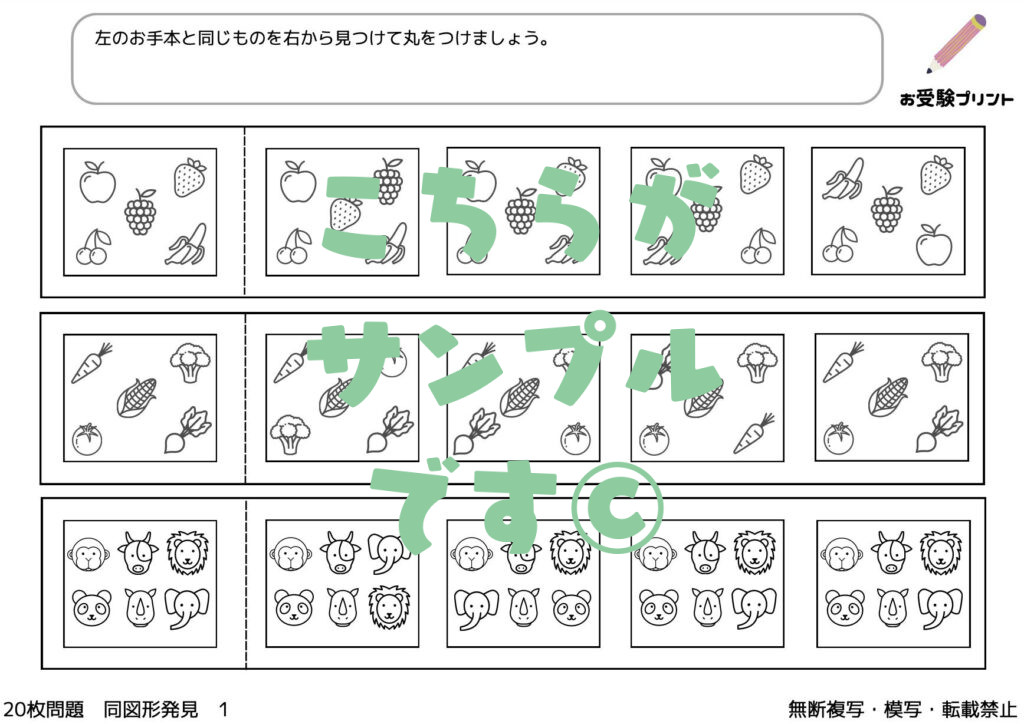
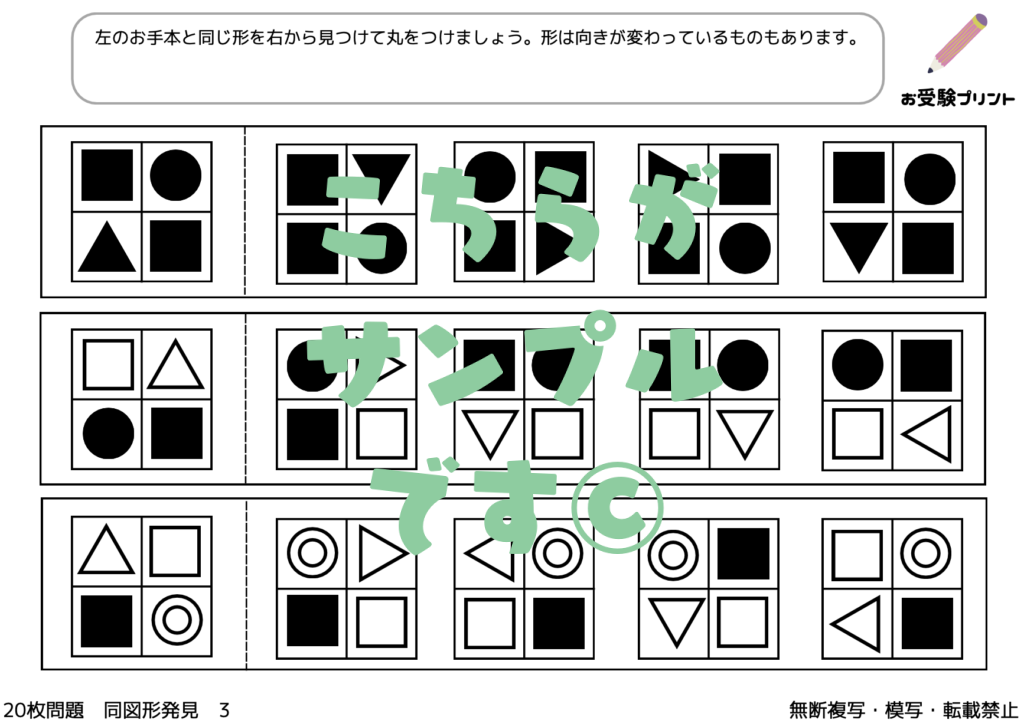
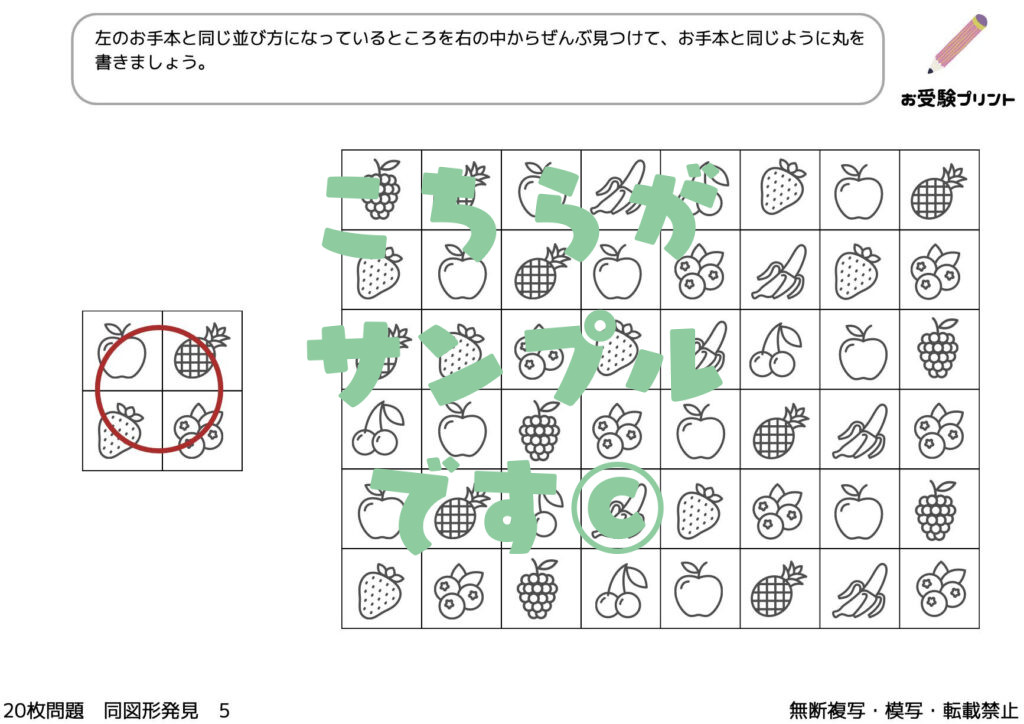
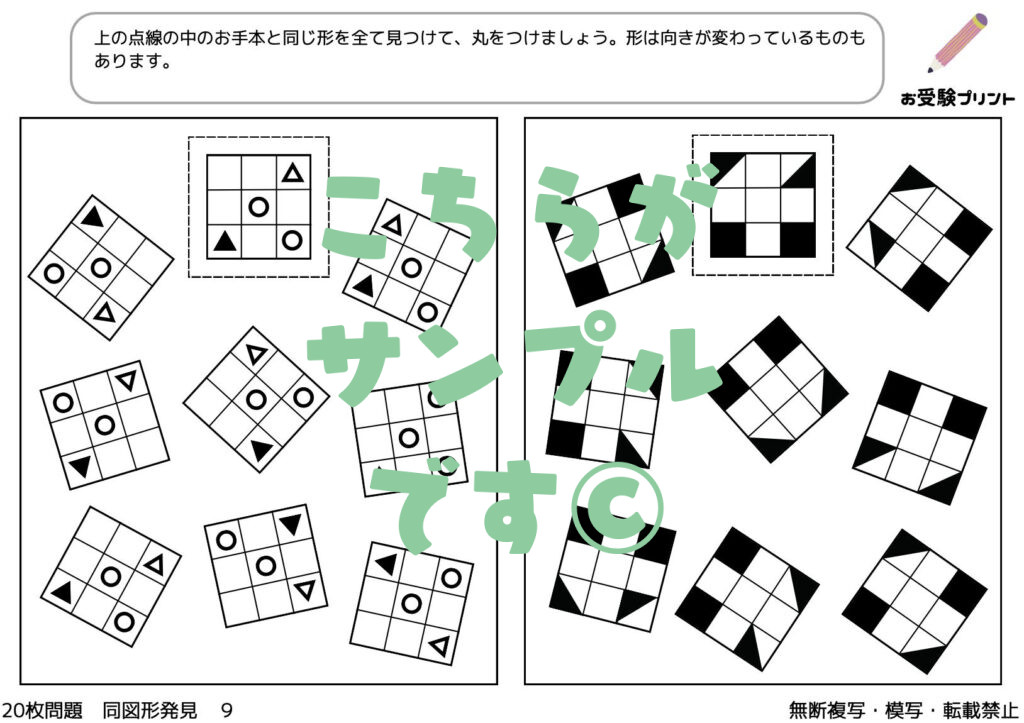
「同図形発見」は、複数の図形の中から同じ形の図形を見つけ出す問題です。
この問題は、一見すると簡単そうに見えますが、実際には子供の観察力、集中力、そして空間認識力を問う非常に奥深いものです。受験では、このような問題を通じて、子供たちが図形をどのように認識し、違いや共通点を見つける能力が求められます。
図形の形を認識するためには、いくつかのポイントに注目することが重要です。例えば、角の数や直線と曲線の配置、対称性など、図形の基本的な特徴を理解することが求められます。
これらを把握することで、子供たちは視覚的なパターンを効果的に認識し、同じ図形を見つけることが可能になります。
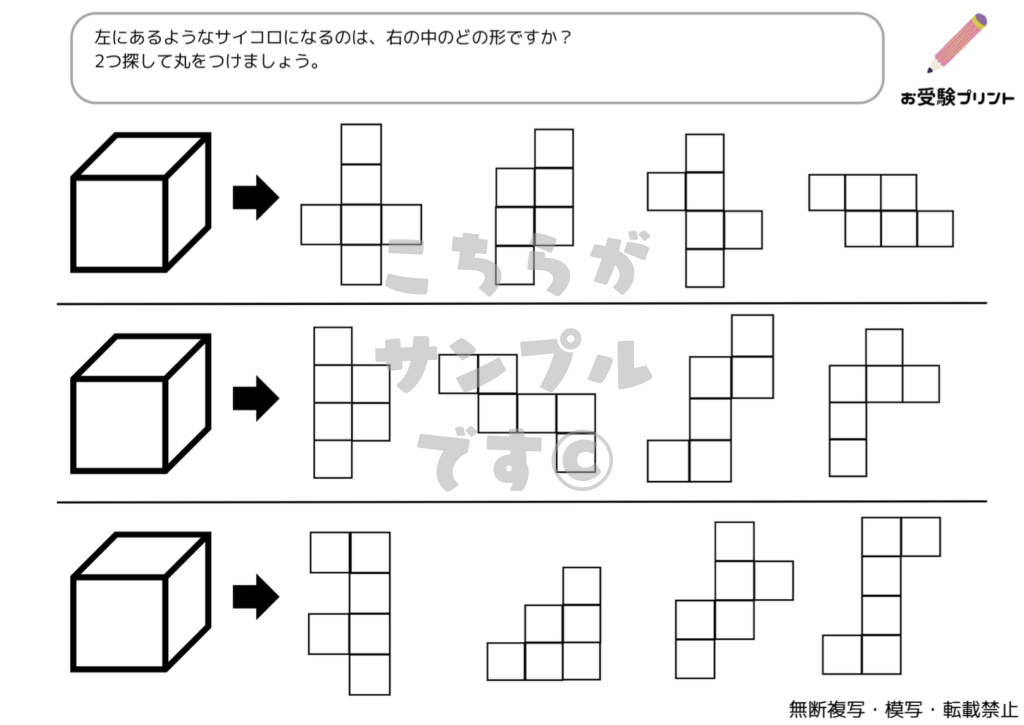
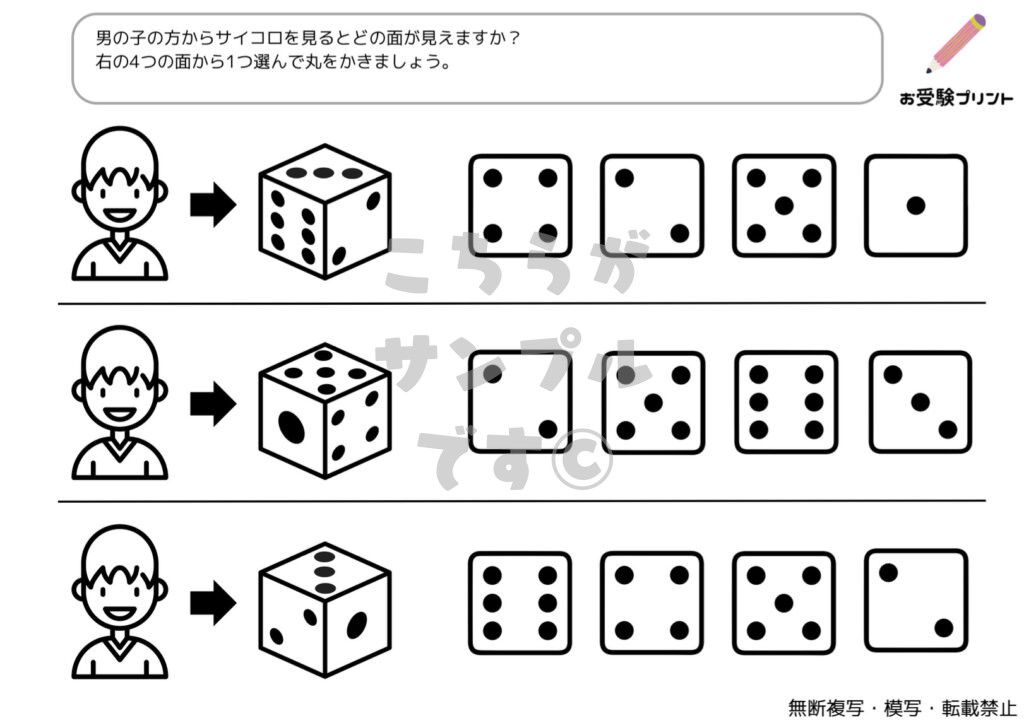
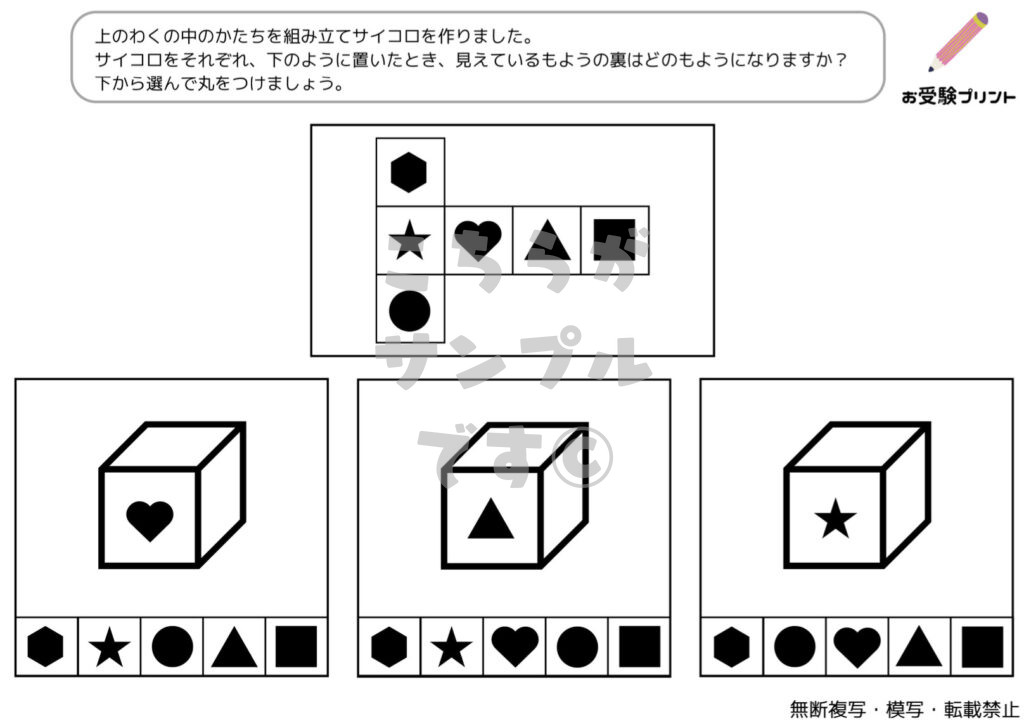
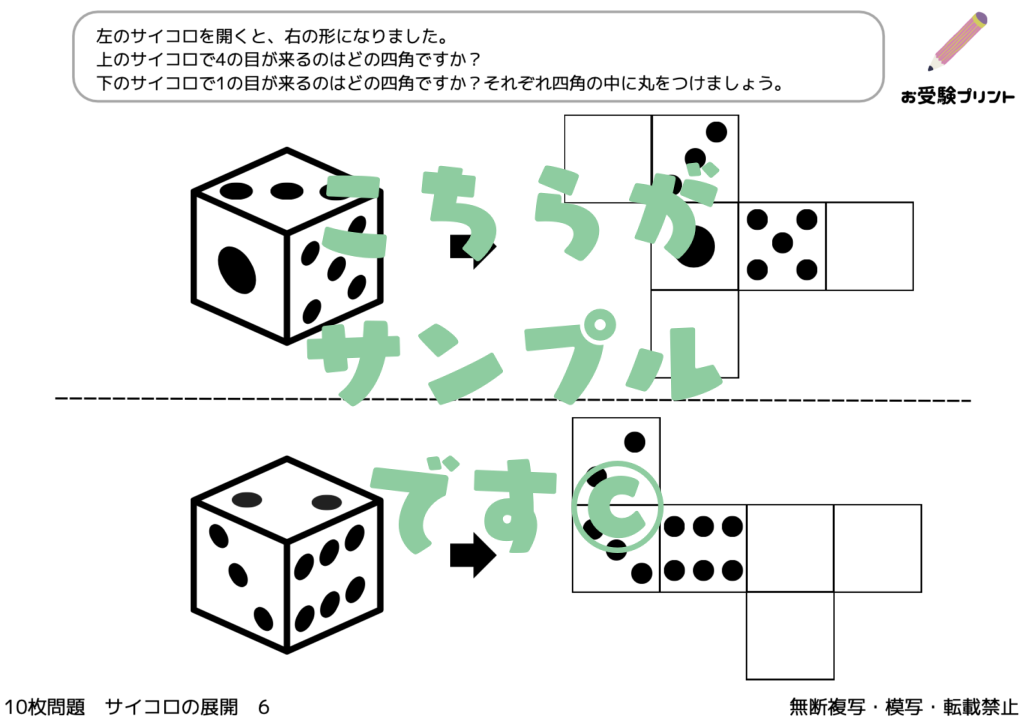
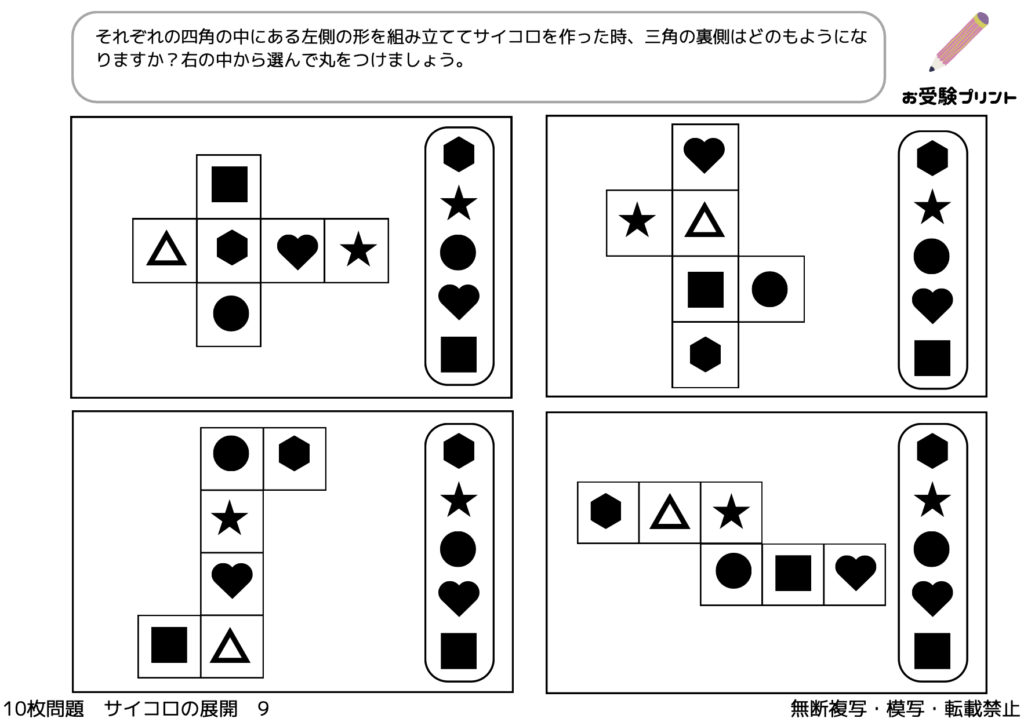
サイコロの展開とは、一言で言うと、立体のサイコロを平面に広げた形のことを指します。これは小学校受験の問題としてよく出題され、子供たちの空間認識能力を試すための一つです。
具体的には、サイコロの各面には1から6までの数字があり、それぞれの面がどのように接しているのかを理解することが求められます。例えば、サイコロを一つの平面に展開したとき、どの数字がどの数字と隣り合っているのか、または反対になるのかを予測する能力が問われます。
このような問題は、子供たちが立体と平面の関係を理解し、また視覚的な情報を解釈する能力を育てるのに非常に有効です。また、この問題を解くことで、子供たちは論理的思考や問題解決能力を鍛えることができます。
サイコロの展開の問題に取り組むことは、子供たちが自分の思考を形にするための一つの手段となります。そして、それは受験だけでなく、日常生活においても役立つスキルとなるでしょう。
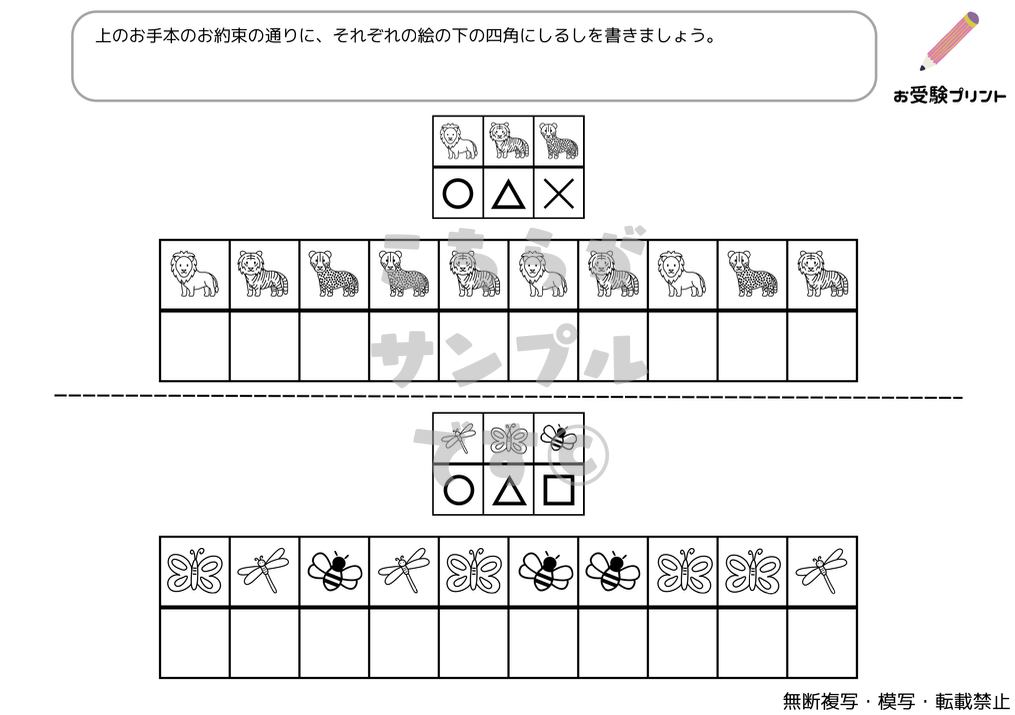
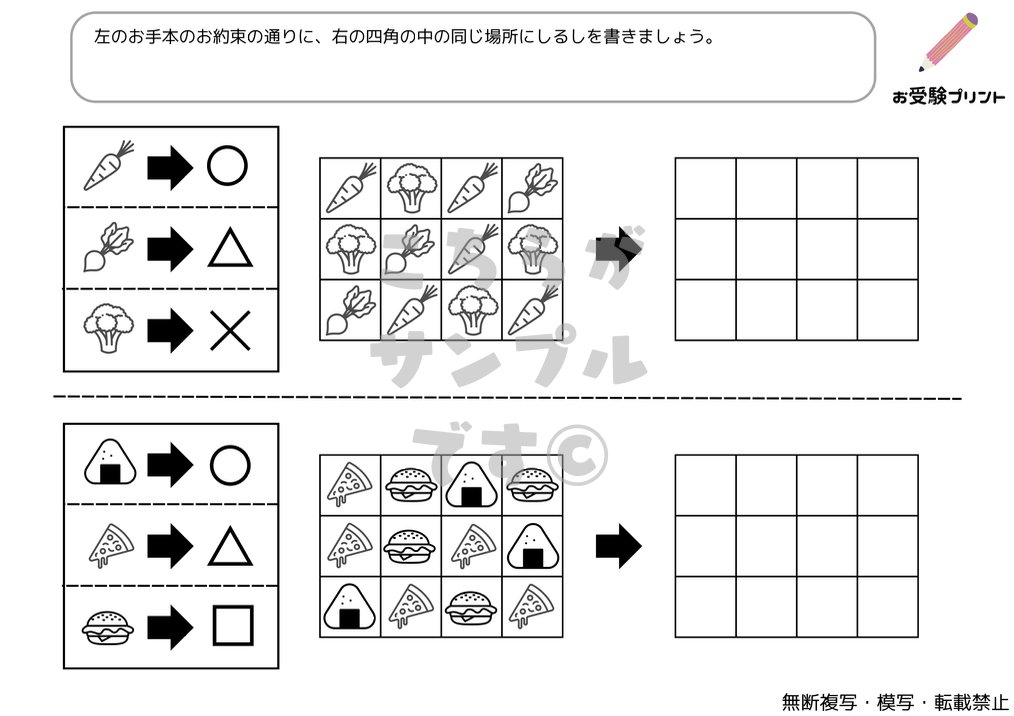
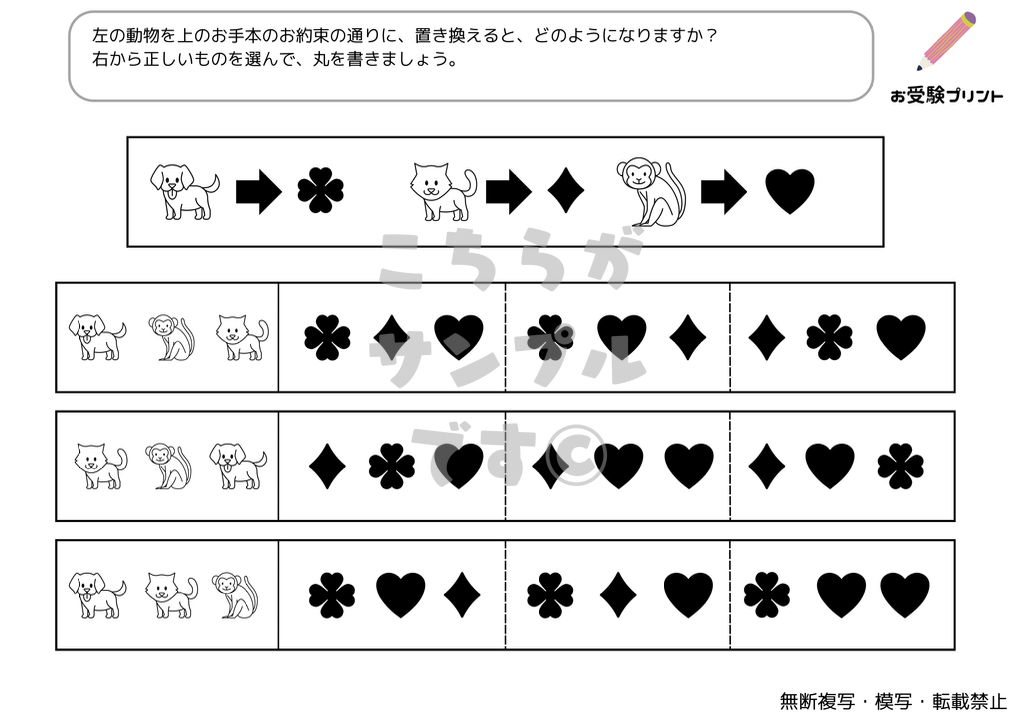
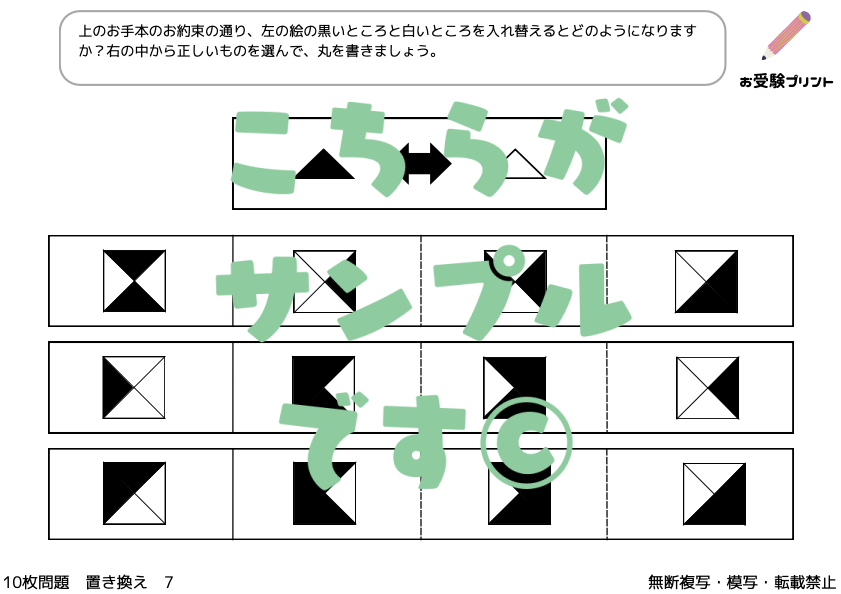
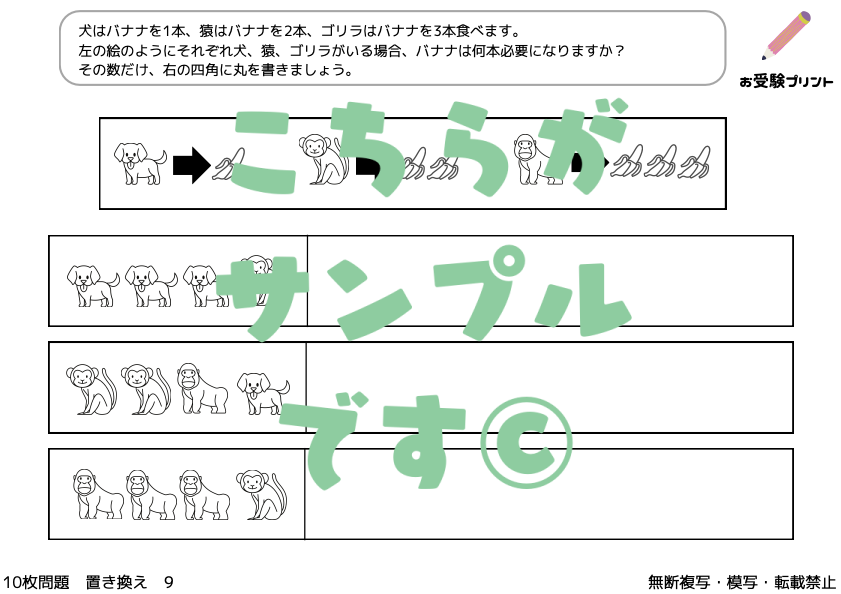
「おきかえ問題」とは、特定のルールに基づいてアイテムを置き換える問題を指します。この問題は、子供たちが論理的思考力と推理力を鍛えるのに非常に有効です。具体的には、ある状況や条件が与えられ、その中で特定のアイテムを別のアイテムに置き換えるというものです。これにより、子供たちは複雑な問題を解決するためのスキルを身につけることができます。
この種の問題は、初めて取り組む子供たちにとっては難易度が高いかもしれません。そのため、親御さんが子供をサポートし、問題解決のプロセスをガイドすることが重要です。また、繰り返し練習することで、子供たちは徐々に「おきかえ」問題の解き方を理解し、自信を持って取り組むことができるようになるでしょう。
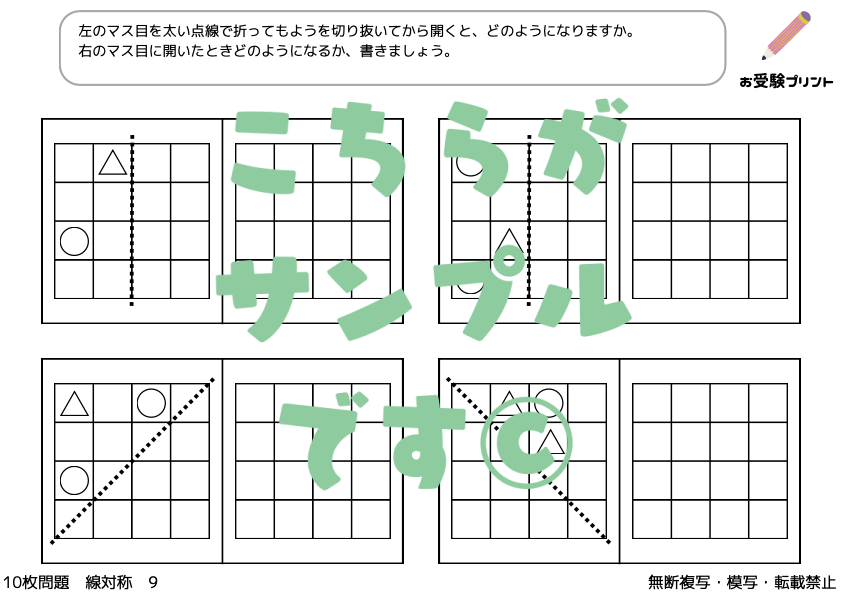
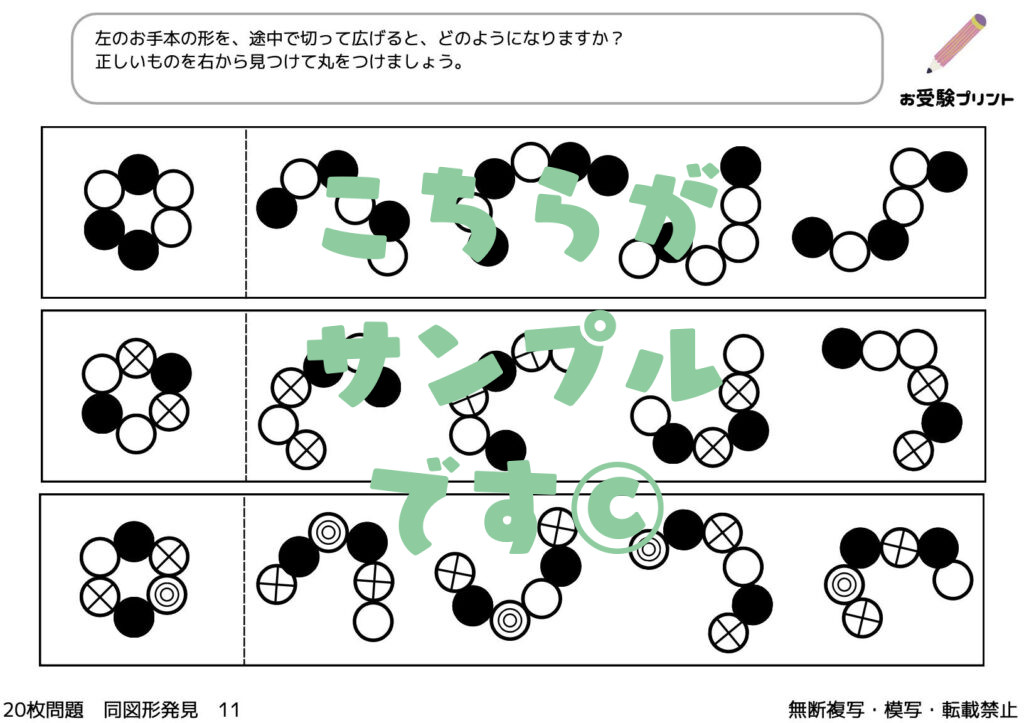
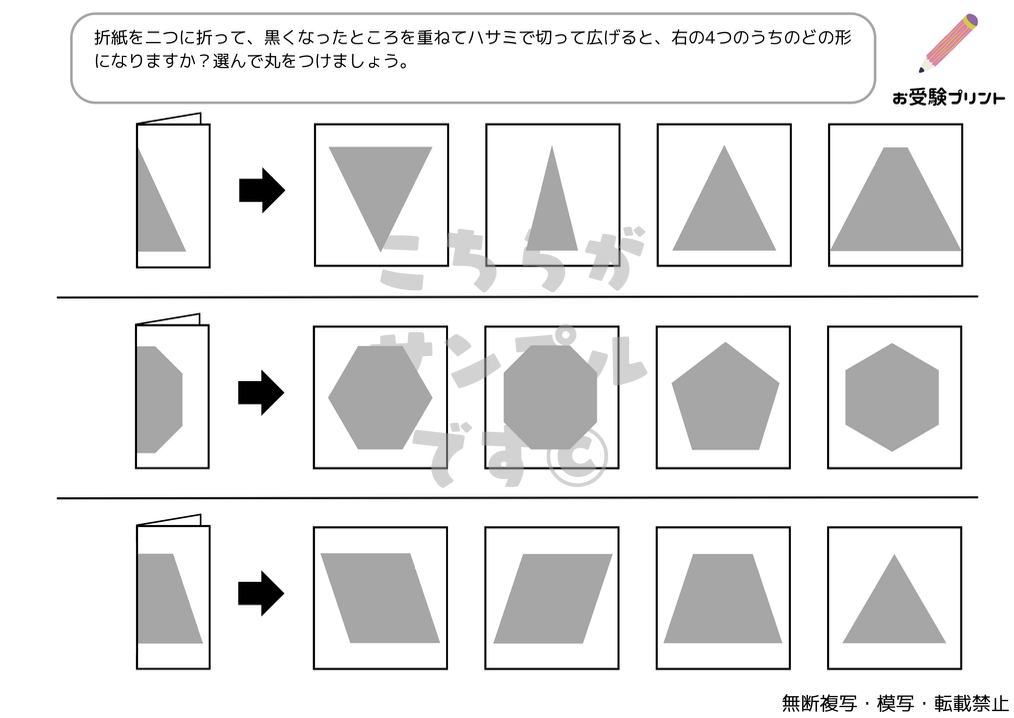
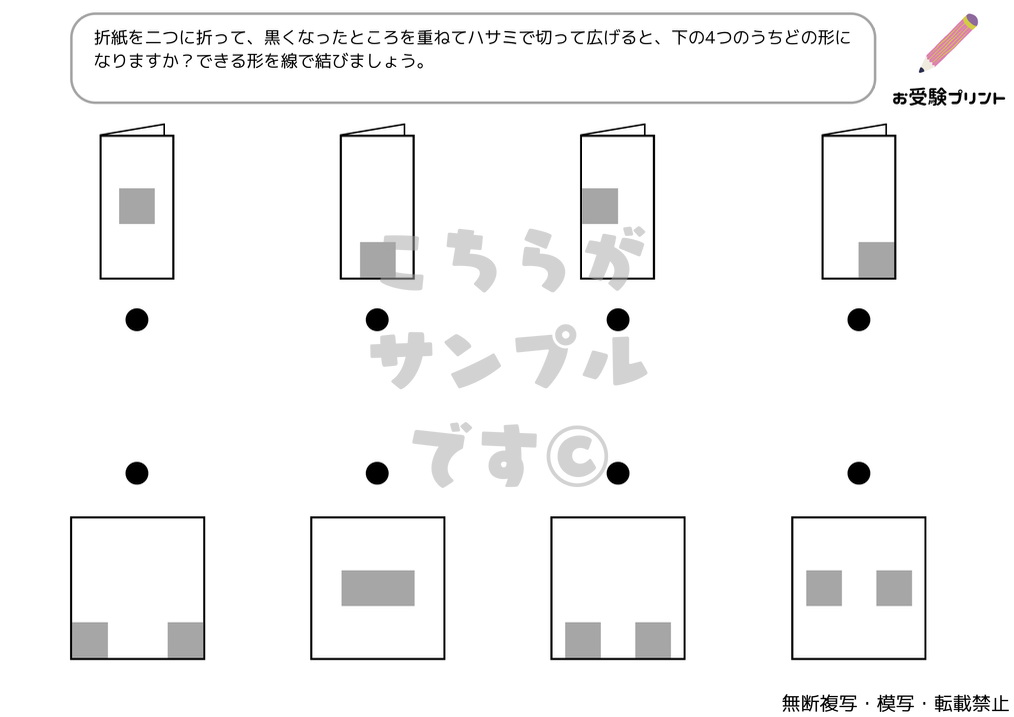
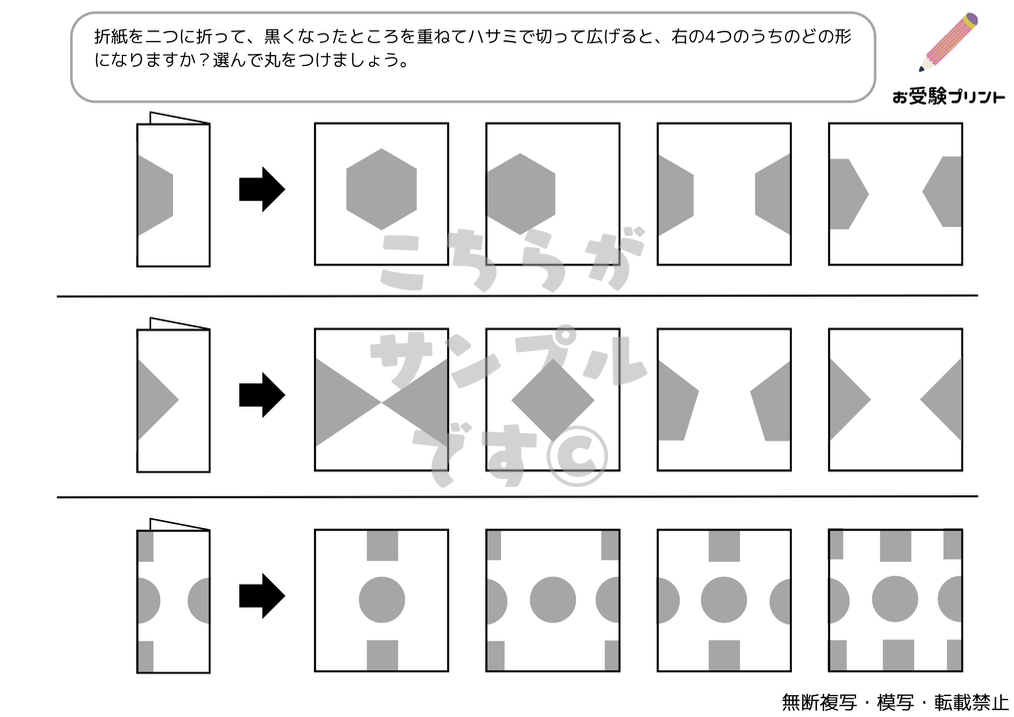
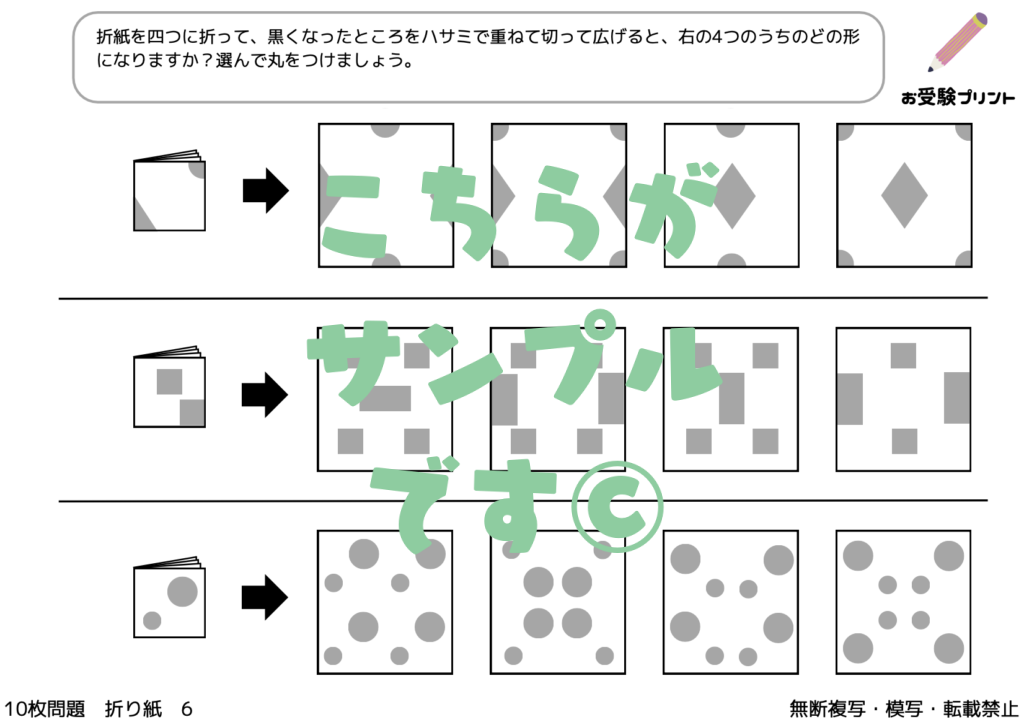
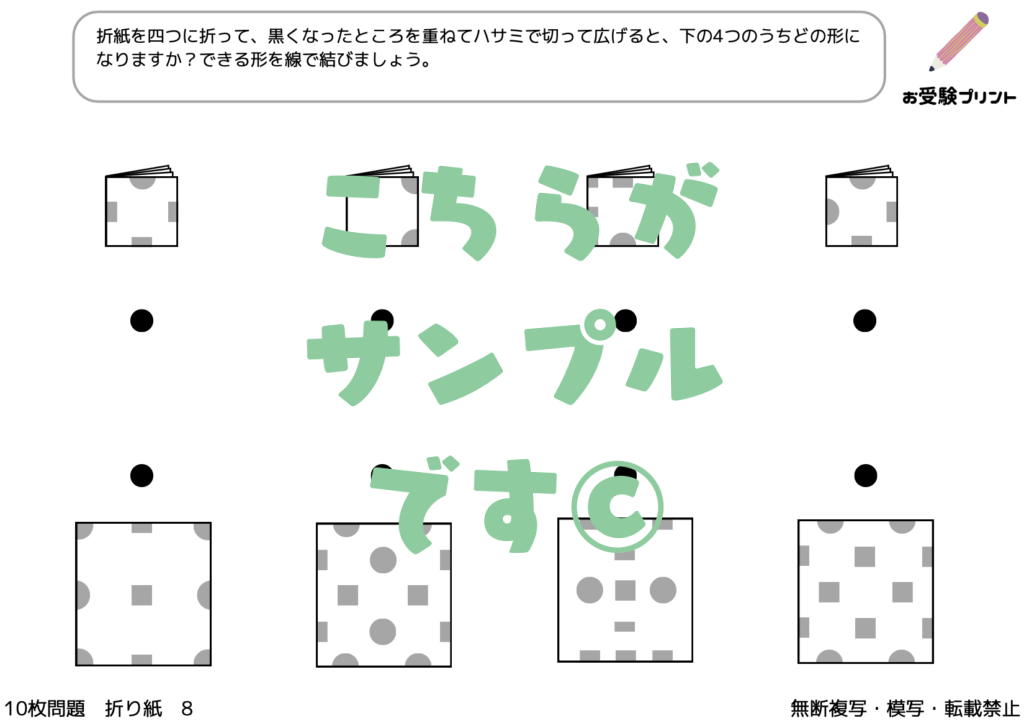
「折り紙の展開図」問題は、子供たちに、折り紙を畳んだ状態で一部を切り取り、それを開いた時にどのような図形が現れるかを予測させる問題です。
この問題は、折り紙を畳む方法（2つ折り、4つ折りなど）と切り取る位置によって、様々な図形が生成されます。
例えば、折り紙を2つ折りにして中央に切り込みを入れると、開いた時には対称的な形が現れますが、複雑な4つ折りの場合は予測がより難しくなります。
このタイプの問題は、子供たちにとって、単に図形を理解するだけでなく、空間的な思考力や創造力、そして推理力を試す機会となります。
また、この問題は、折り紙の畳み方や切り方によって無限のバリエーションが生まれるため、子供たちの想像力を豊かにすることにも繋がります。
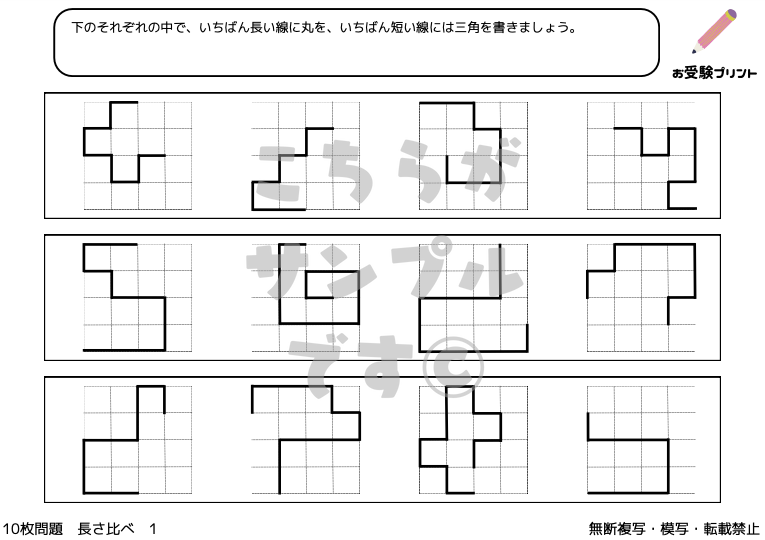
「長さ比べ問題」とは、複数の物体の長さを比較し、その順序を回答する問題です。
この種類の問題は、子供たちにとって直感的に取り組みやすいように思えますが、実際には物体間の相対的な長さを把握し、それを論理的に整理する能力が求められます。
小学校受験では、この問題を通じて子供の観察力、比較能力、そして論理的思考力を評価することが一般的です。
具体的には、直線や物体の実際の長さを比較して、最も長いもの、短いもの、あるいは中間の長さのものを順に並べるという形式がよく使われます。
この過程では、視覚的情報を処理し、それを基に推論を展開するスキルが重要になってきます。
また、問題によっては、実際に手を動かして測定することから、複雑な思考を要する比較まで、さまざまな形式があります。
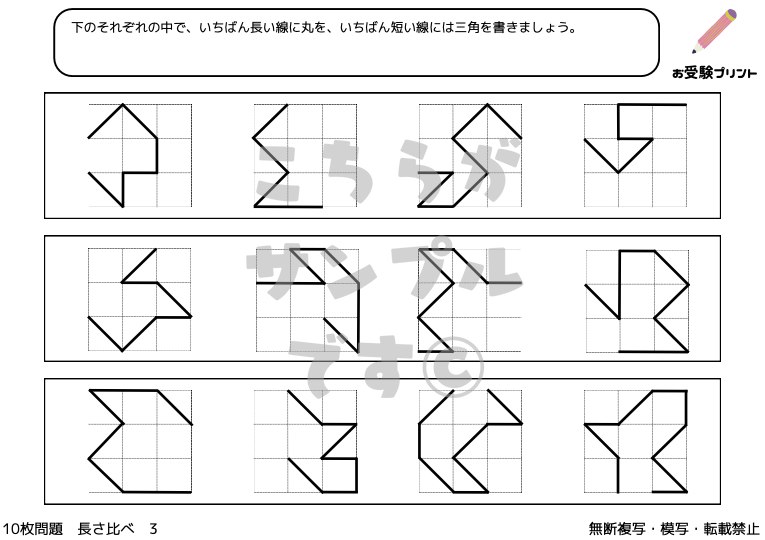
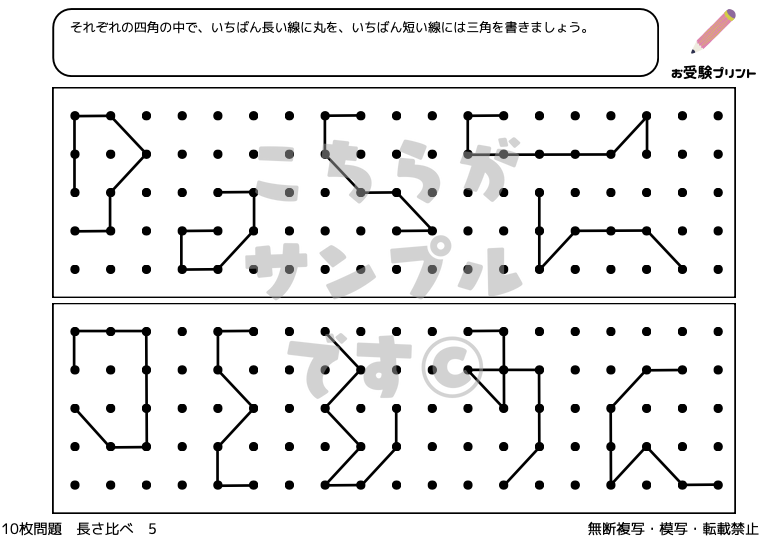
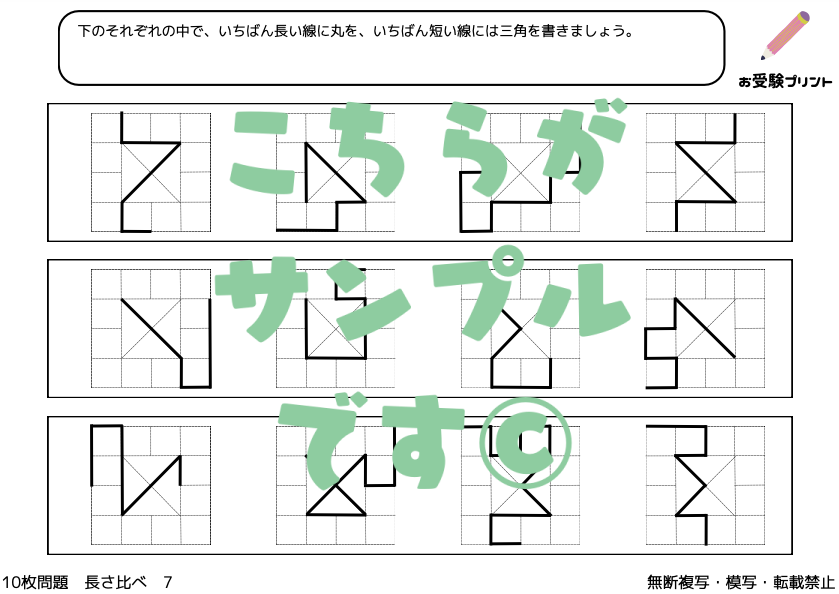
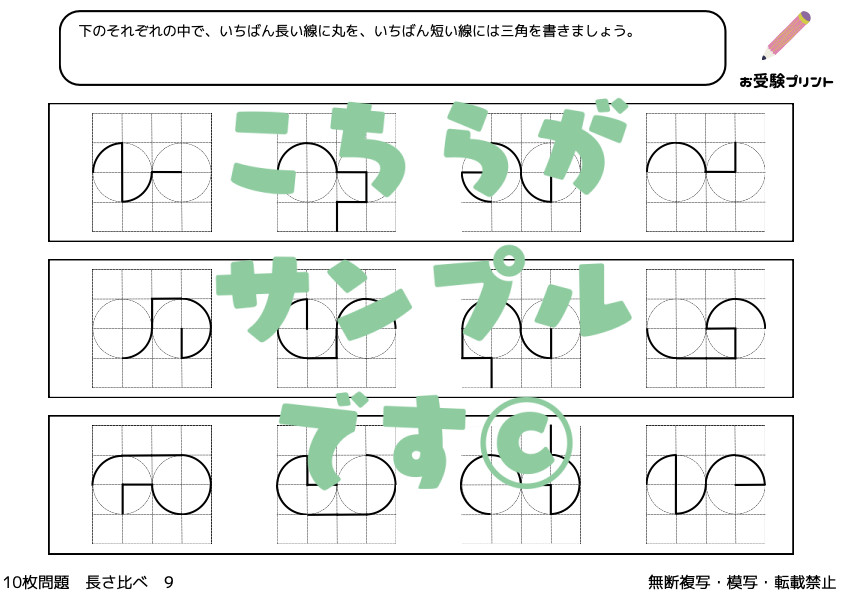
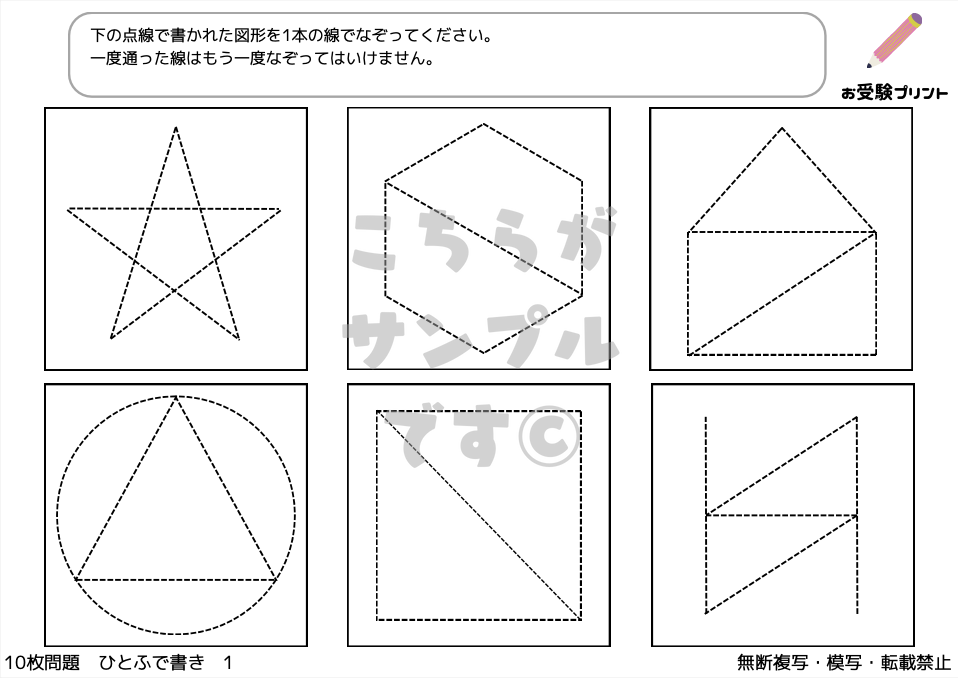
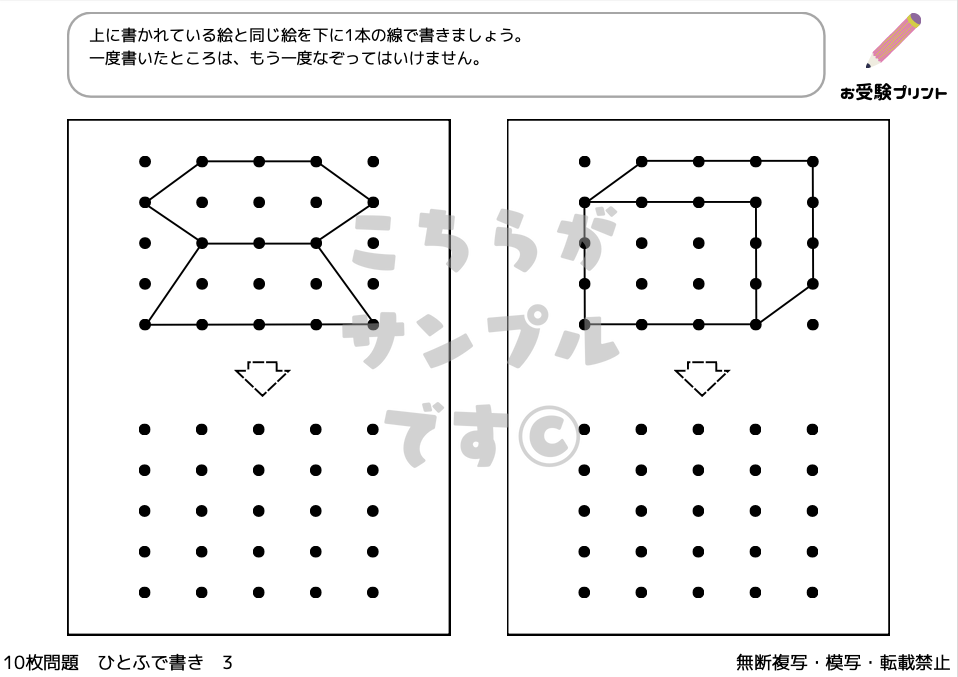
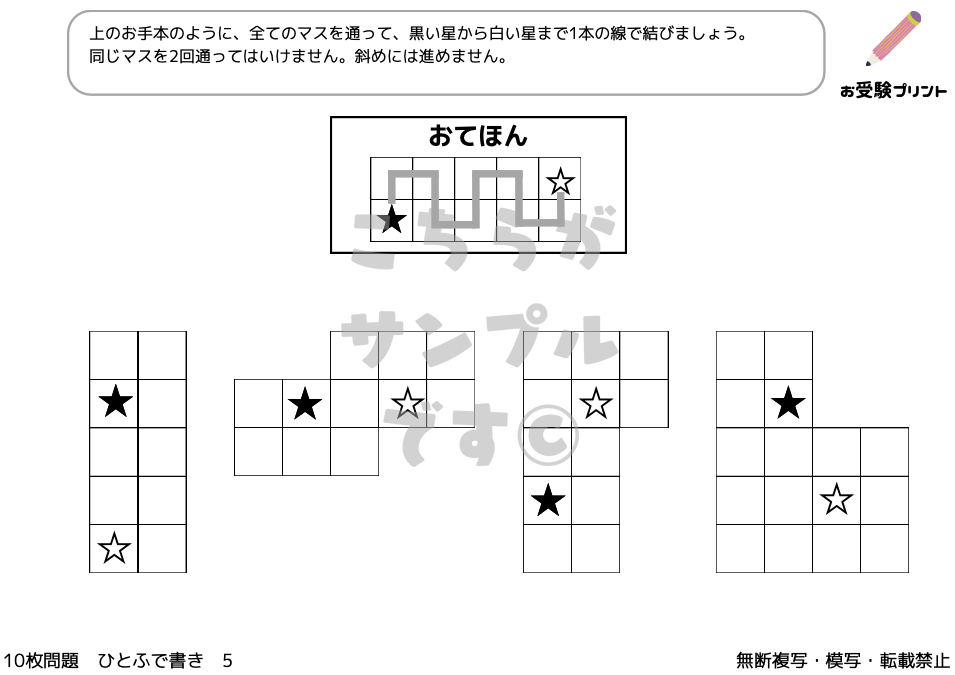
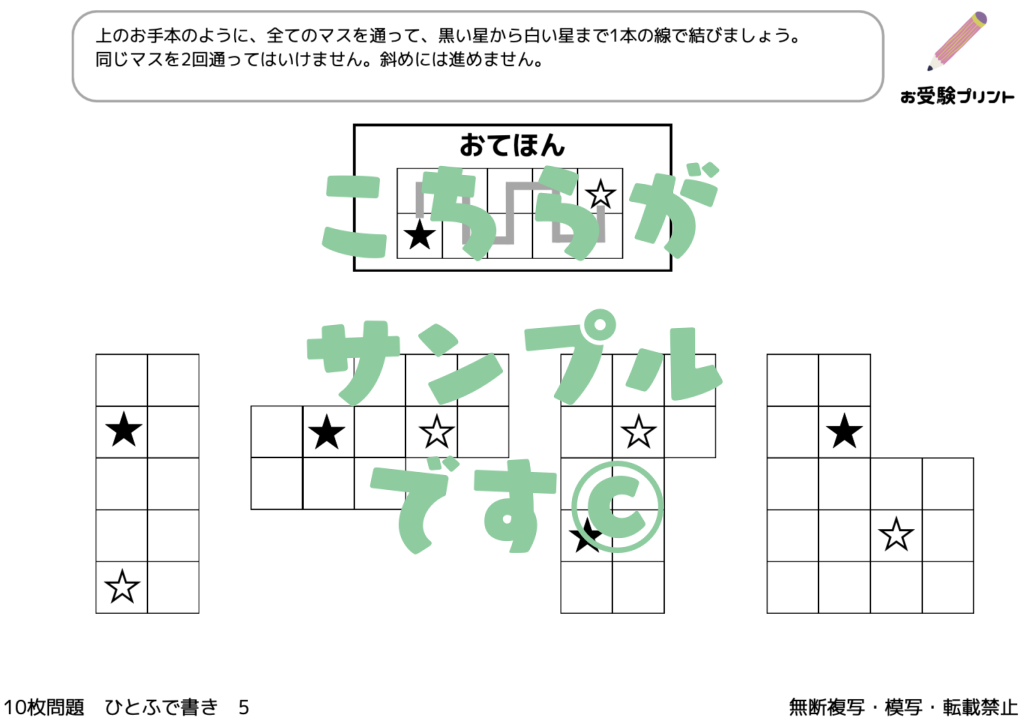
「一筆書き問題」とは、全ての線を一度ずつだけ通り、すべての点を結ぶ問題です。
この問題の魅力は、そのシンプルさにありますが、解くためには論理的な思考が必要です。
始点から出発し、切れ目なく一筆で全ての線を辿り、最終的に終点に至るルートを見つけ出すことが目標です。
多くの場合、一筆書き問題には特定のルールが設けられており、それらのルールの下で最適な解答を見つけることが求められます。
子供たちにとって、この問題は思考力を養うだけでなく、計画性や先読みの能力を試す絶好の機会となります。
また、問題を解く過程で試行錯誤を重ねることが、論理的思考能力の向上につながり、学習意欲を刺激します。
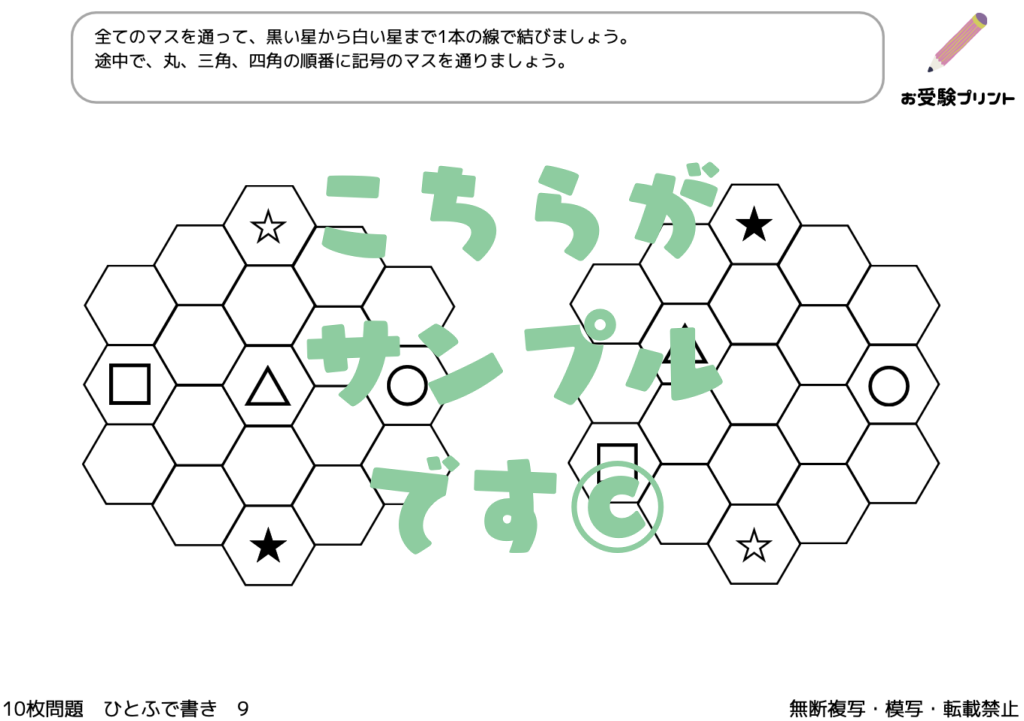
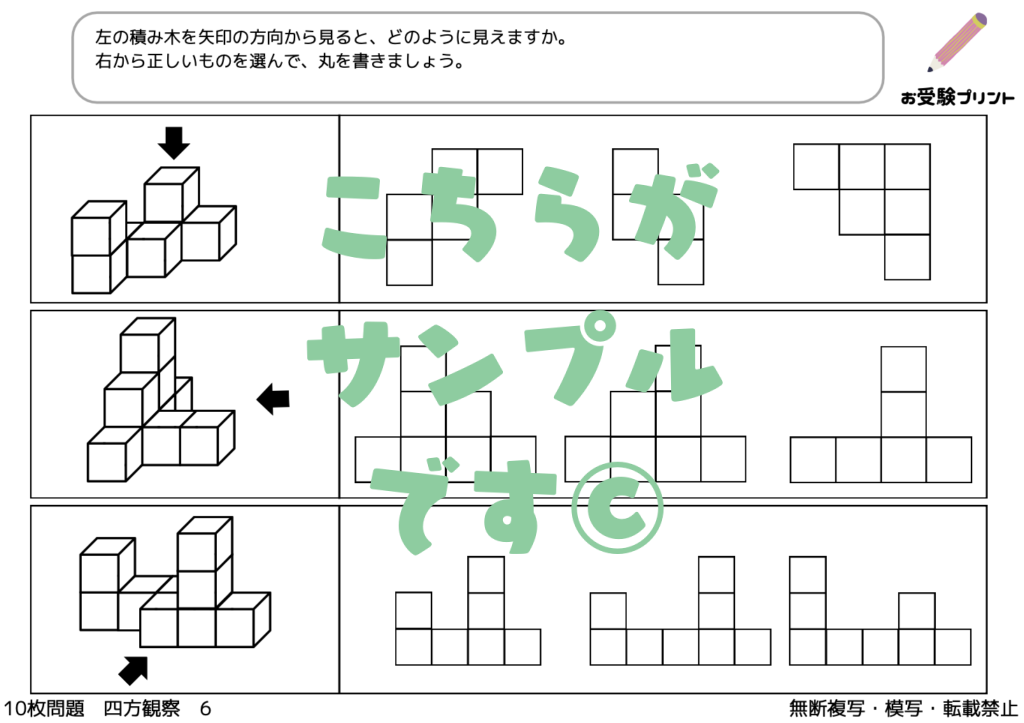
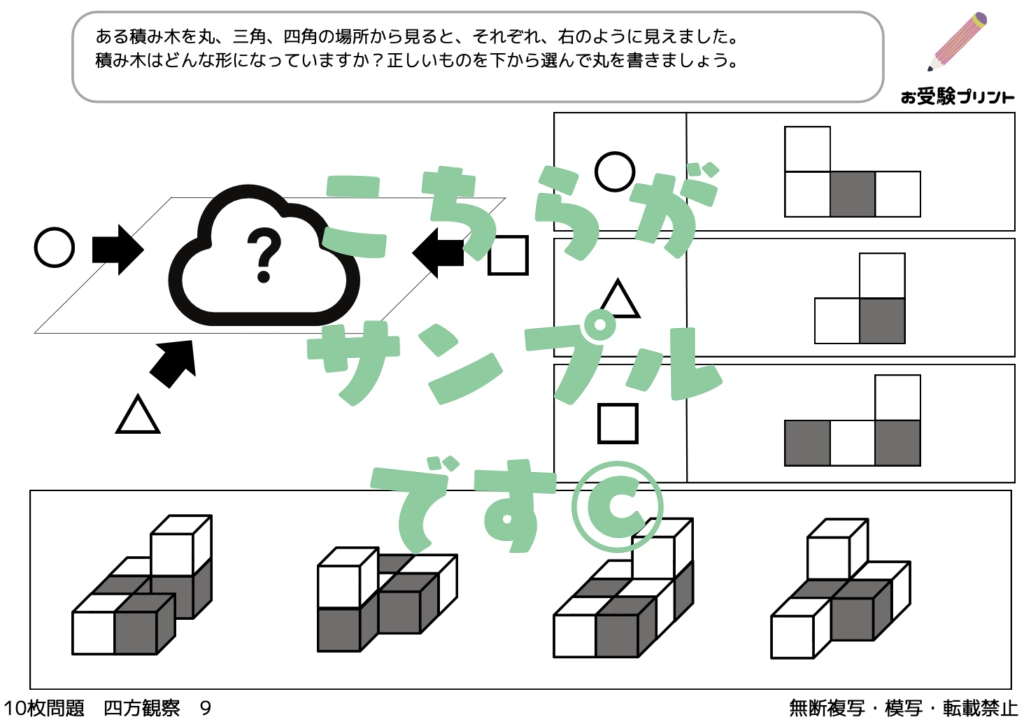
見え方の推理とは、物事を視覚的に理解し、それを基に推理する能力を問う問題です。具体的には、図形や模様、色の配置などを見て、そのパターンや規則性を見つけ出し、それを用いて未知の情報を推測することを求められます。
例えば、ある図形が次々と変化していく様子を見て、次にどのような図形になるのかを予測する問題などがあります。また、色の配置や模様の変化から、その背後にある規則性を見つけ出し、それを基に未知の情報を推測する問題もあります。
このような問題は、視覚的な情報を理解し、それを基に論理的に思考する能力を鍛えることができます。また、視覚的な情報から規則性を見つけ出す能力は、日常生活や学習においても非常に重要なスキルです。
小学校受験においては、このような見え方の推理問題が出題されることがあります。受験生は、図形や模様の変化を正確に理解し、それを基に論理的に思考する能力を身につけることが求められます。
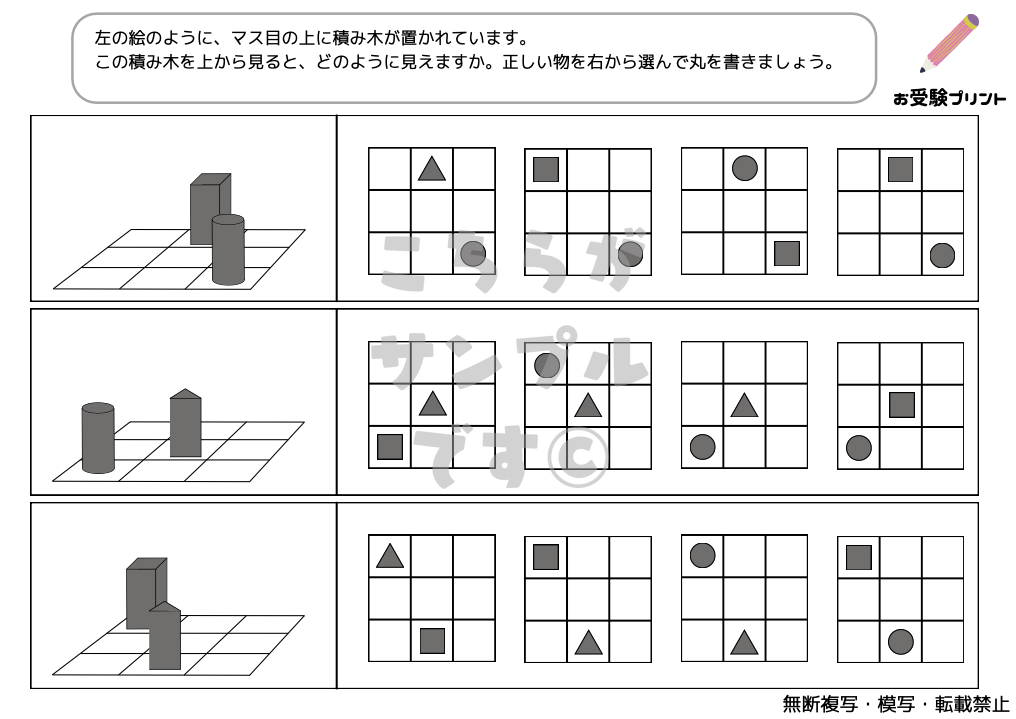
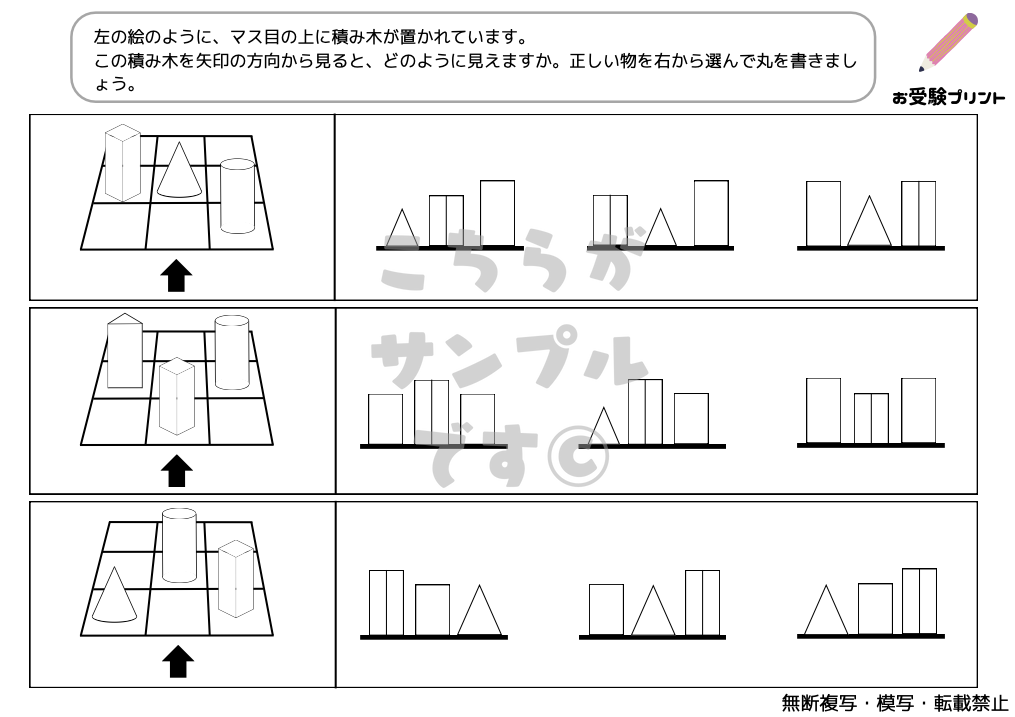
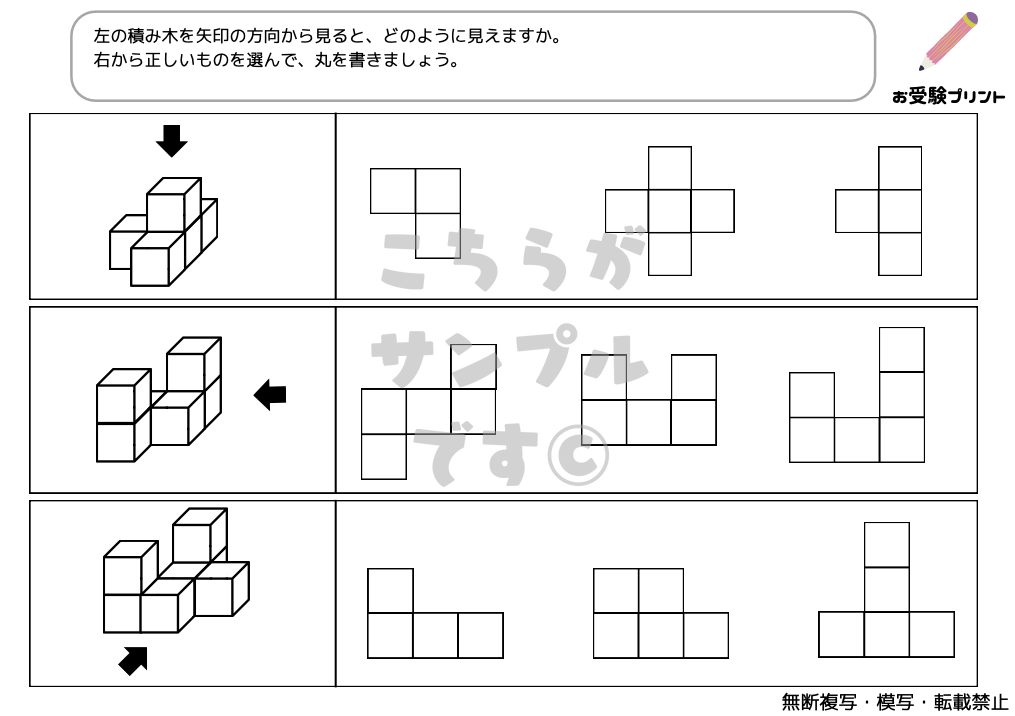
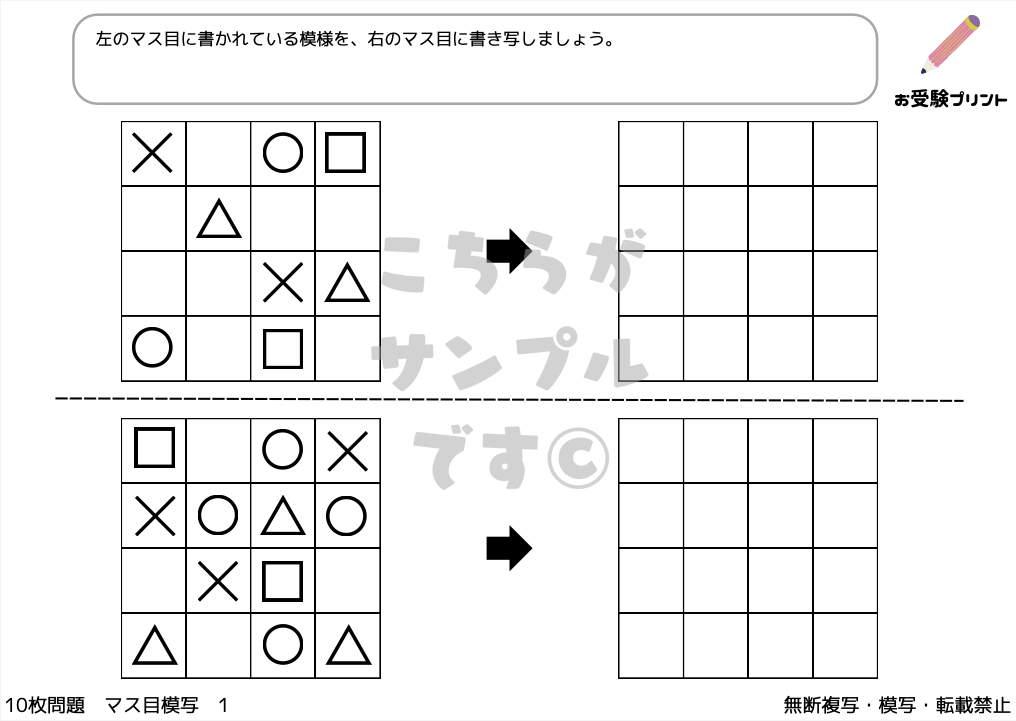
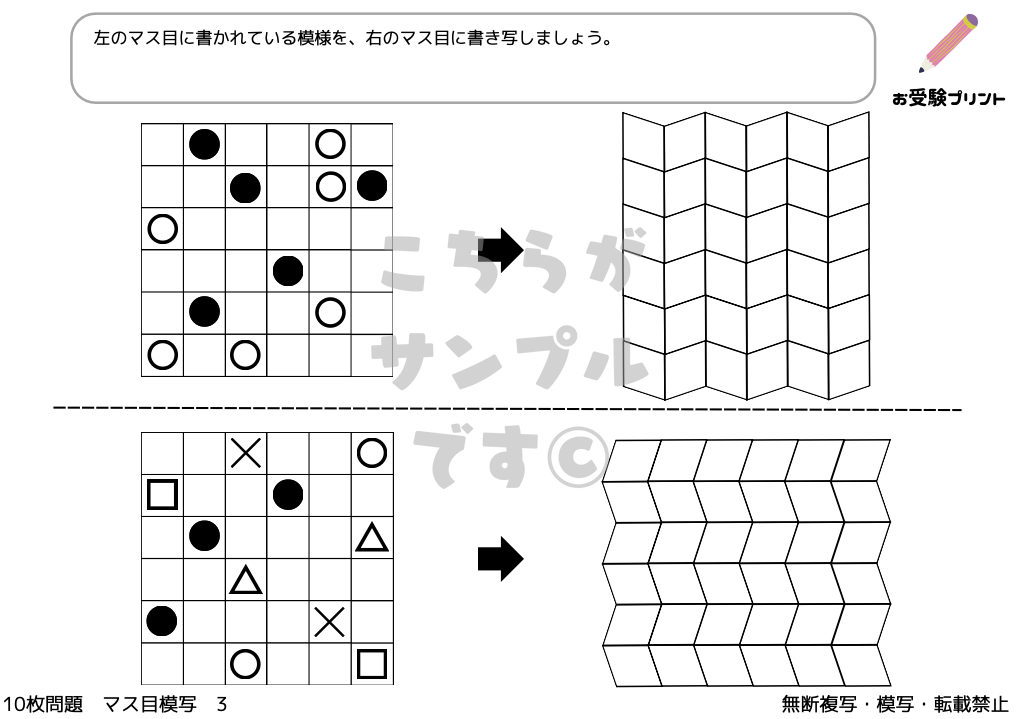
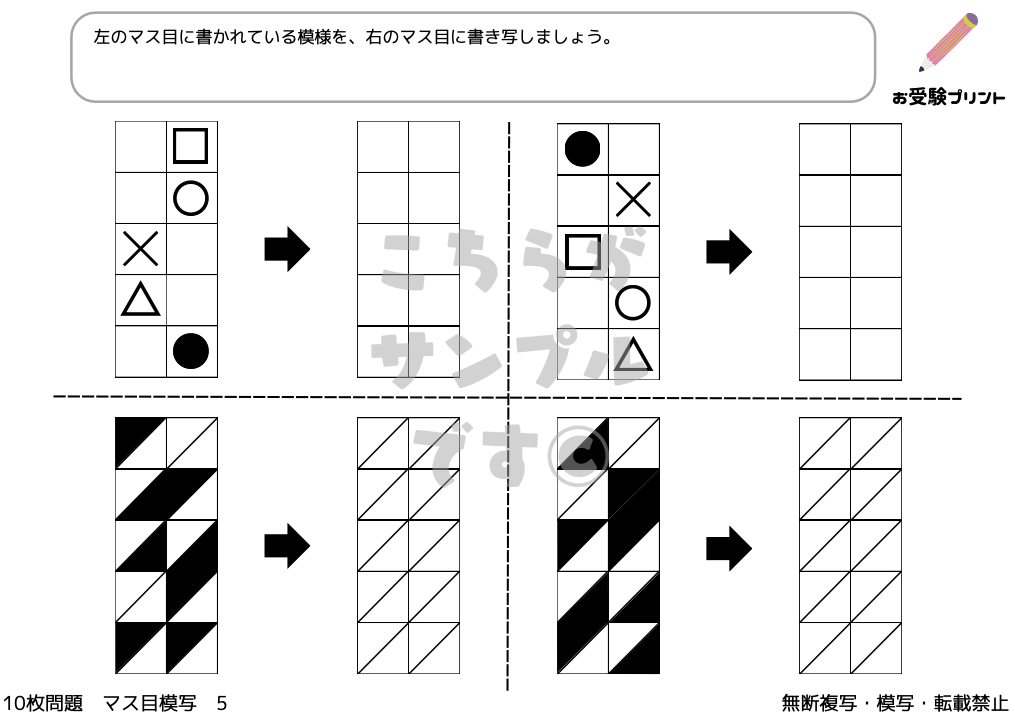
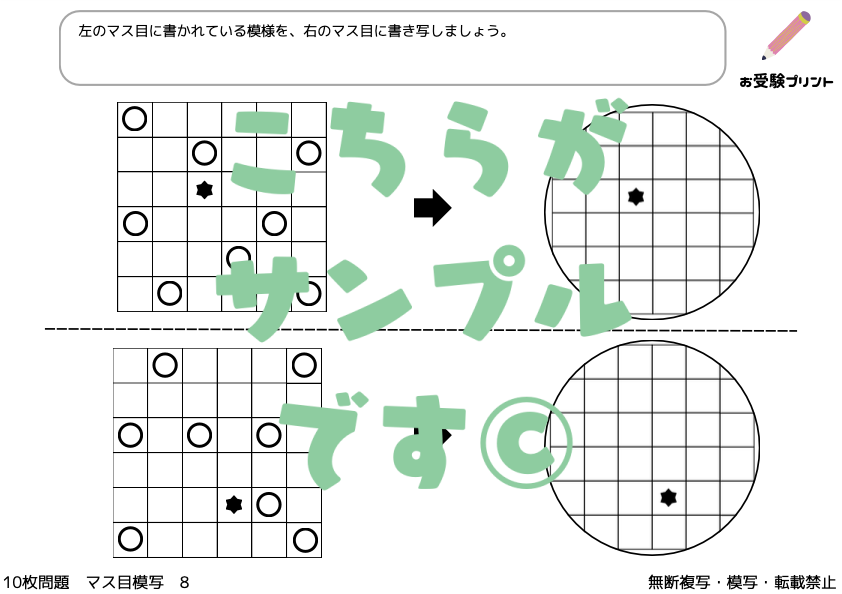
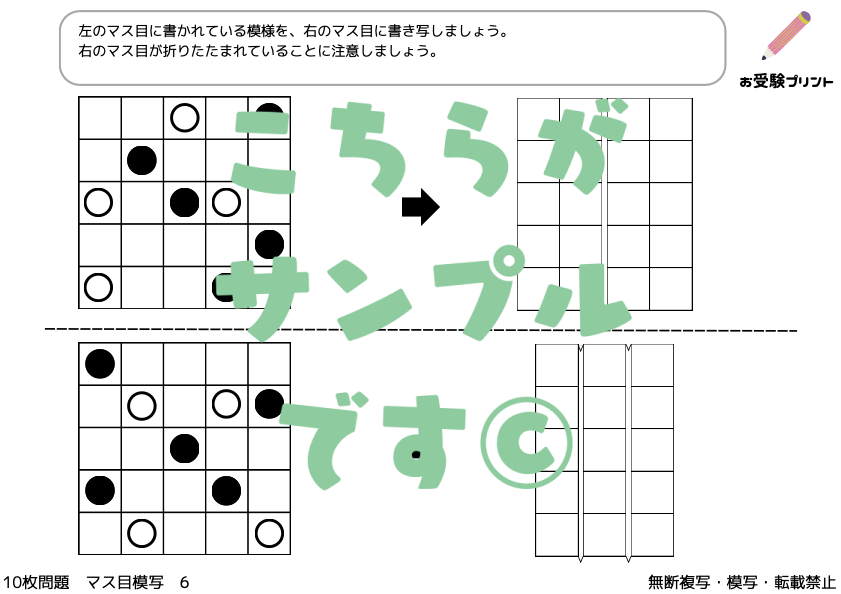
「マス目模写問題」は、子供たちの観察力、集中力、そして細かい動作の制御能力を養うための重要な練習です。
方眼用紙に不規則に描かれた印や図形を、別の方眼用紙に精密に書き写すこの問題は、子供たちが細部に注意を払いながら、空間的な理解を深めるのに役立ちます。
また、マス目模写問題は、子供たちの論理的思考力や問題解決能力を高めるのにも有効であり、小学校受験において非常に重要な要素となっています。
この問題を通して、子供たちは自身の思考プロセスを整理し、より効率的な学習方法を身につけることができます。
数の問題は、小学校受験において非常に重要な部分を占めています。数の概念を理解し、それを基に計算や数列のパターンを把握することは、論理的思考を育てる上で欠かせません。ここでは、数の問題の基本的な解き方と、その中でも特に重要なポイントを解説します。
数の概念を理解することは、計算力を身につける第一歩です。まずは、数の基本的な性質や、足し算・引き算といった基本的な計算を理解しましょう。また、数の合成という概念も重要です。これは、ある数を他の数の組み合わせで表すことを指します。例えば、「5」は「2+3」や「4+1」のように表すことができます。このように数の合成を理解することで、数の関係性やパターンを見つける力が養われます。
子供が苦労するポイントとしては、数の概念自体が抽象的であるため、具体的なイメージを持つことが難しい点が挙げられます。ここでは、具体的な物や図を用いて数を表すことで、数の概念を視覚的に理解することが推奨されます。
教え方のポイントとしては、まずは具体的な物を使って数を数えることから始め、その後徐々に抽象的な数の概念に移行すると良いでしょう。また、数の合成については、日常生活の中で自然と経験する機会を作ることが大切です。例えば、「5つのリンゴを2つと3つに分ける」といった具体的なシチュエーションを想定すると良いでしょう。
数列やパターン、系列といった問題は、数の関係性を理解し、論理的思考を鍛える上で非常に重要です。数列とは、一定のルールに基づいて並べられた数のことを指します。例えば、「2, 4, 6, 8, …」は「2ずつ増える数列」であり、「1, 2, 4, 8, …」は「2倍になる数列」です。これらの数列からパターンを見つけ出し、次に来る数を予測する能力は、論理的思考力の基礎となります。
子供が苦労するポイントとしては、数列のパターンを見つけることが難しい点が挙げられます。特に、複雑なパターンや間接的な関係性を持つ数列では、そのルールを理解するのが難しくなります。
教え方のポイントとしては、まずは単純なパターンから始め、徐々に複雑なパターンに移行すると良いでしょう。また、数列のパターンを見つけるためには、数と数の間の関係性を意識することが重要です。そのため、数と数の間に何が起こっているのかを具体的に説明することで、子供の理解を深めることができます。
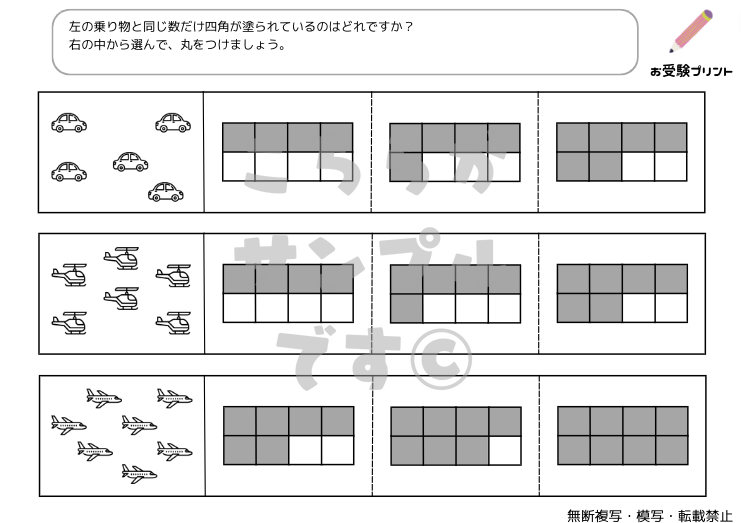
「計数問題」とは、基本的には物事の数を数えることを指します。しかし、小学校受験の観点から見ると、それは単純な数え上げではありません。計数問題は、子供たちが数の概念を理解し、それを適用する能力を試すために重要な問題です。
例えば、「黒タイルを数える」や「円で線を結び、数を数える」などの問題が出題されます。これらの問題は、子供たちが視覚的な情報を解釈し、それを数値情報に変換する能力を試します。また、これらの問題は、子供たちが数の概念を理解し、それを適用する能力を試すために出題されます。
また、計数問題は、子供たちが「どちらがどれだけ多いか」を判断したり、「一人いくつずつ」が何になるかを計算したりすることも含みます。これらの問題は、比較、分配、そしてより複雑な数学的概念への入門となります。
計数は、単に数を数えること以上のものであり、子供たちの数学的思考と理解を育てるための基礎となるスキルを養います。
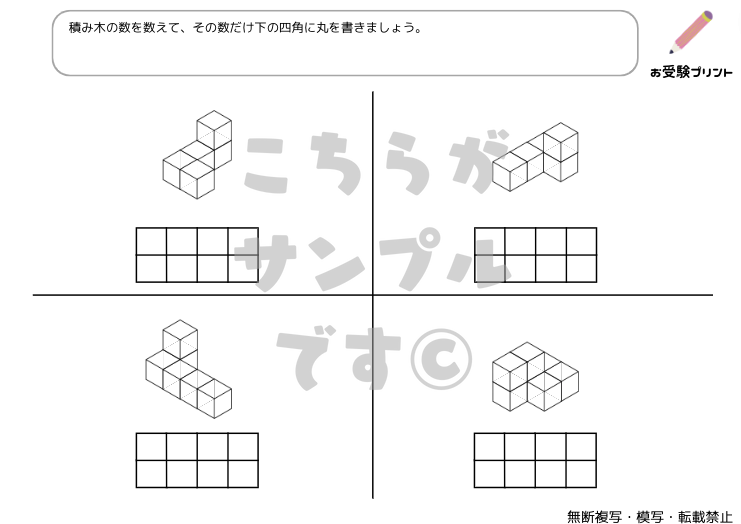
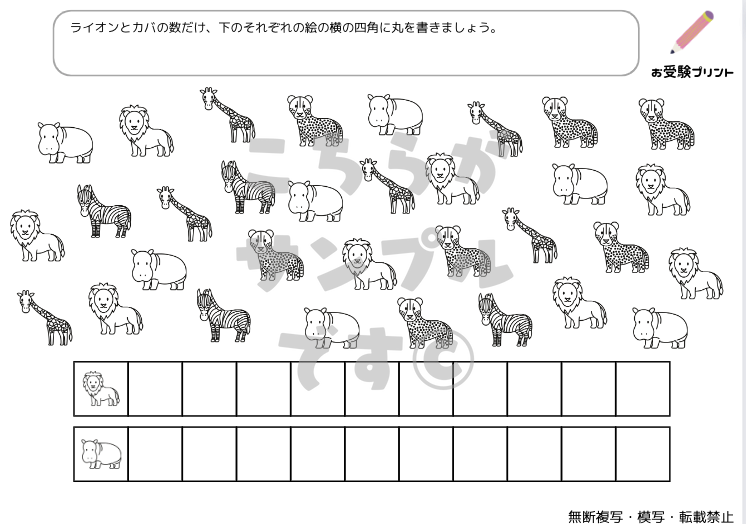
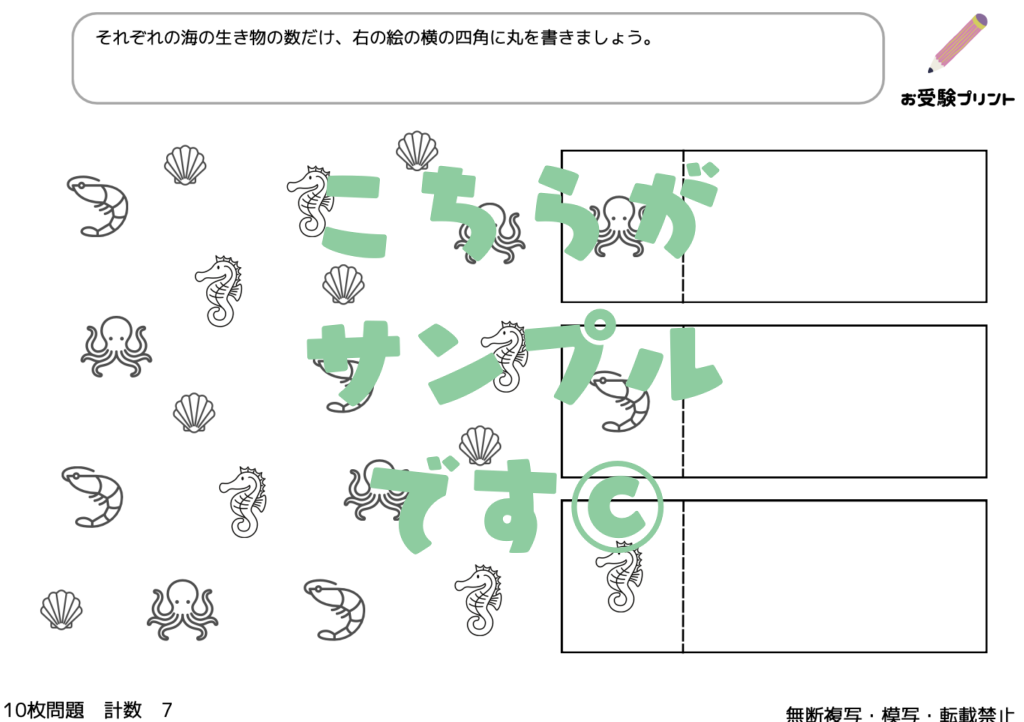
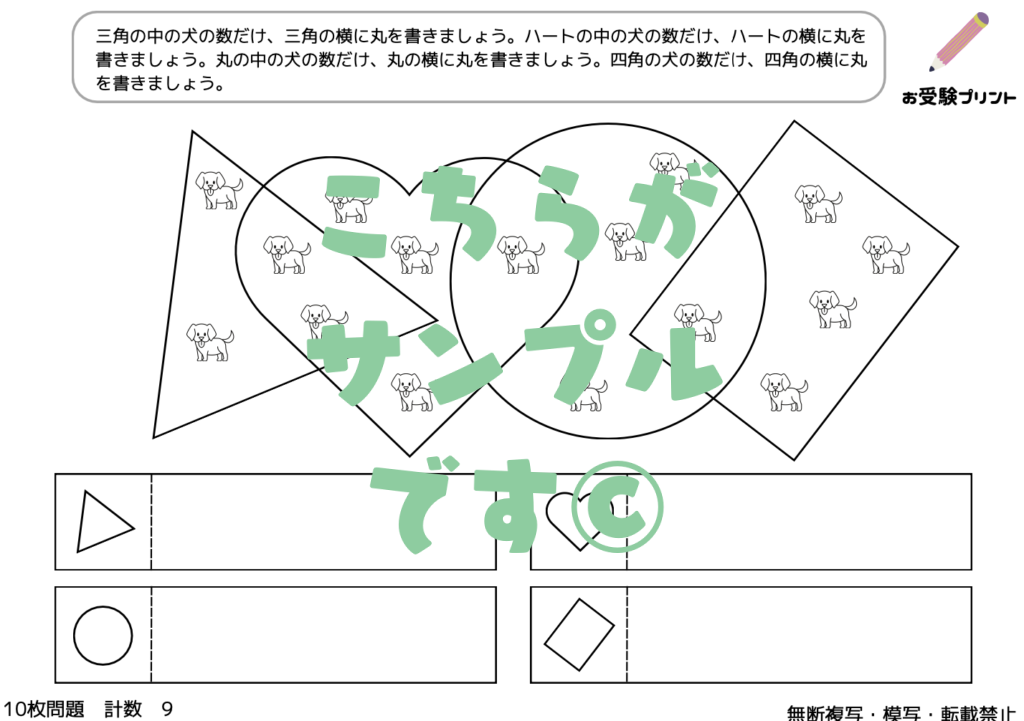
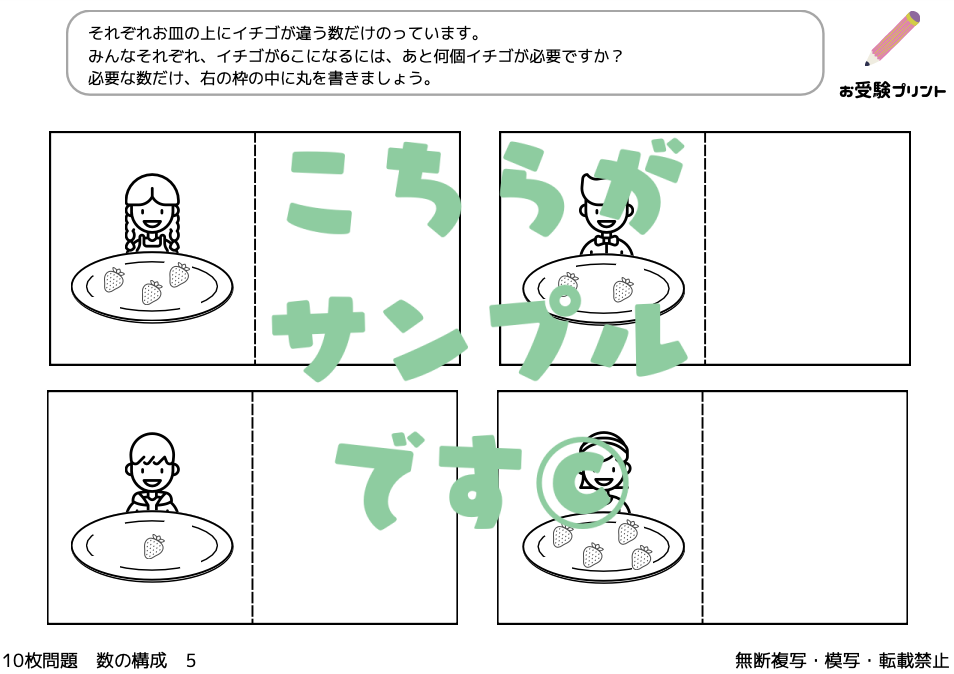
数の構成は、一つの数を他の数の組み合わせで表現する概念を指します。これは、数に対する理解を深めるための基本的なスキルであり、子供たちが将来、より複雑な数学の概念を理解するための土台となります。
また、数の構成は、足し算と引き算の基本的な理解を支える要素ともなります。
数の構成を通じて、子供たちは「合わせていくつになりますか？」や「○個増えるといくつになりますか？」、「○個減ったらいくつになりますか？」、「○個になるにはあといくつ必要ですか？」といった基本的な算数の言葉とその概念を学び、これらの言葉がどのように数学的な計算や問題解決に関連しているのかを理解することが可能になります。
これにより、数の構成は小学校の算数の学習、特に足し算や引き算の理解を深める上で重要な役割を果たします。
これらの理由から、数の構成の学習は、小学校受験の準備期間において重要なテーマとされています。
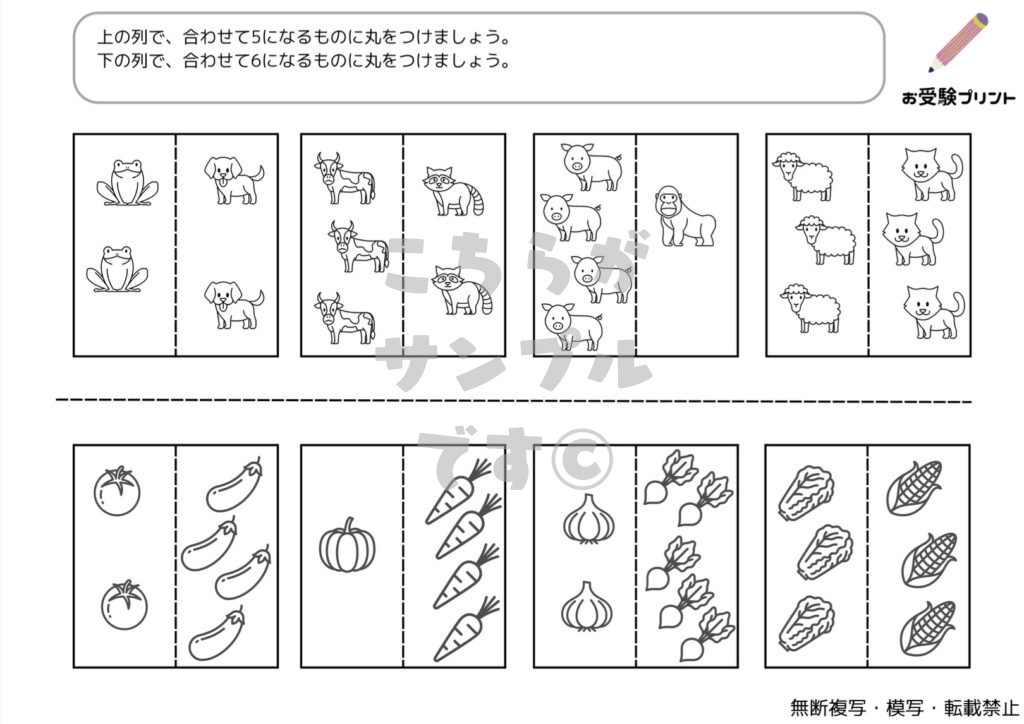
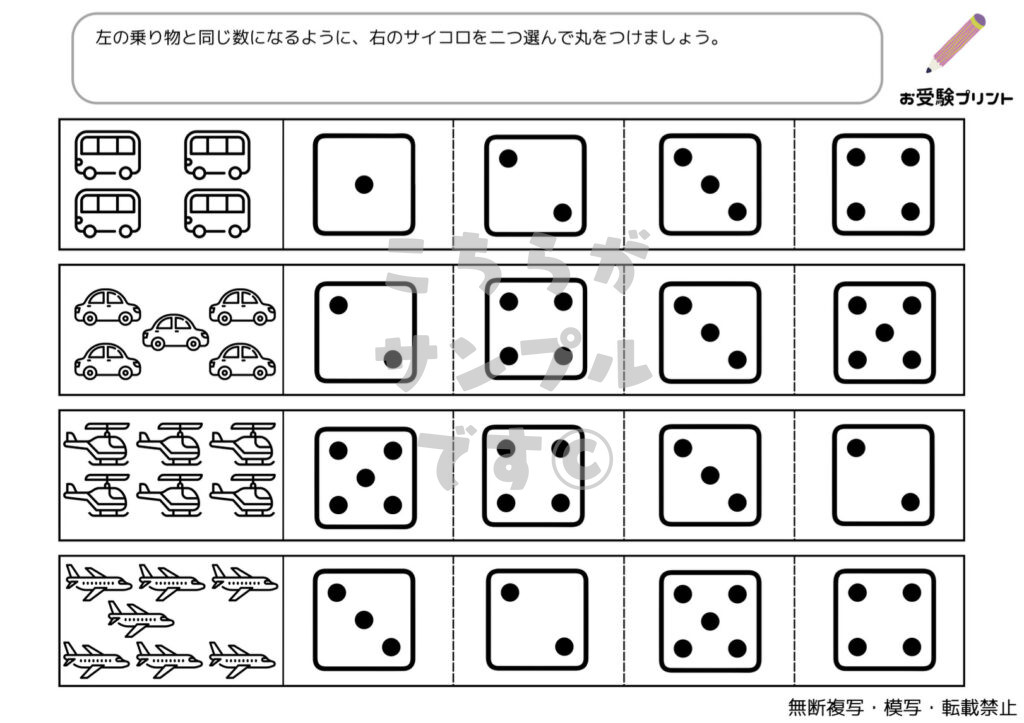
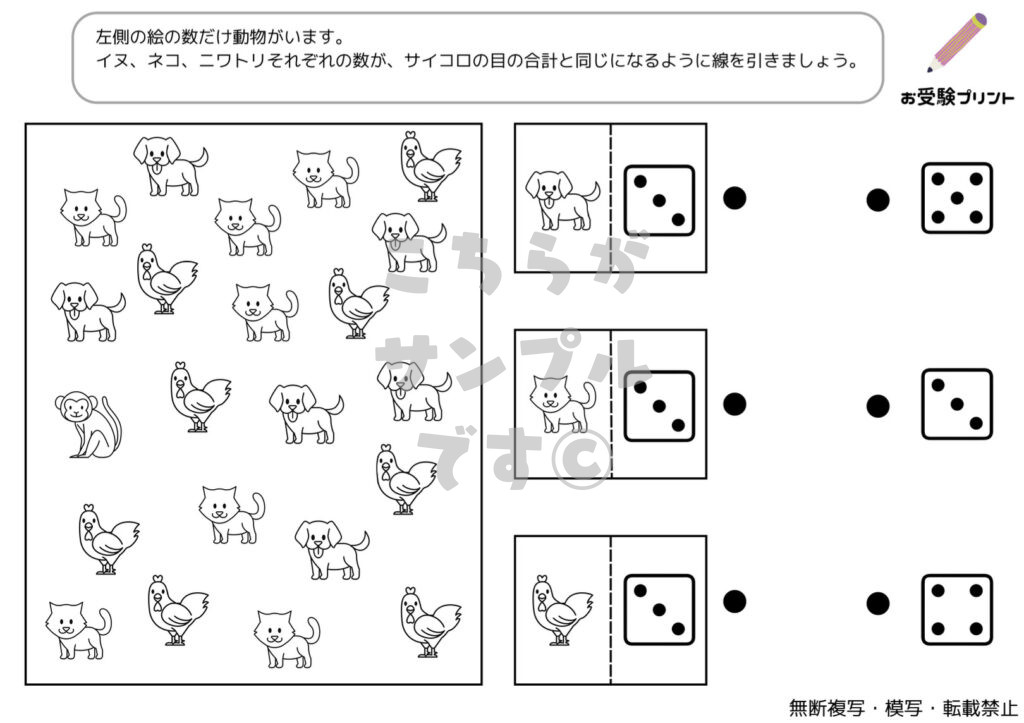
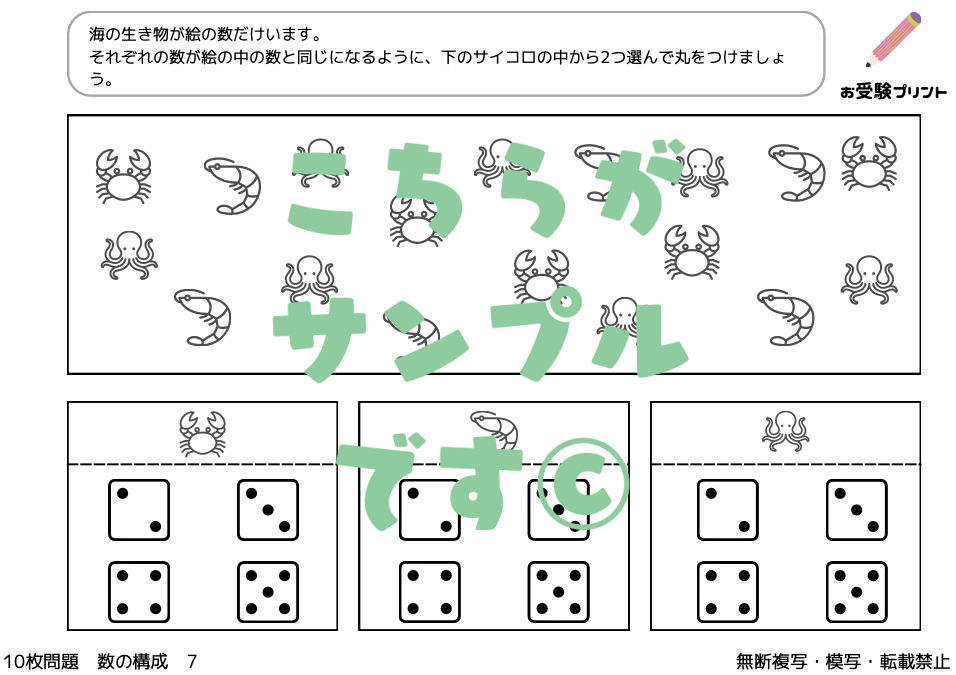
「数の比較•釣り合い」は、小学校受験の問題の一つで、子供たちが数の比較とバランス感覚を学ぶための重要な問題です。具体的には、2つ以上の物体や数値が与えられ、それらがどのように比較され、どのように釣り合っているかを理解し、解答することが求められます。
このような問題は、子供たちが論理的思考や問題解決能力を養うために重要です。また、日常生活における数の理解を深めることも可能です。
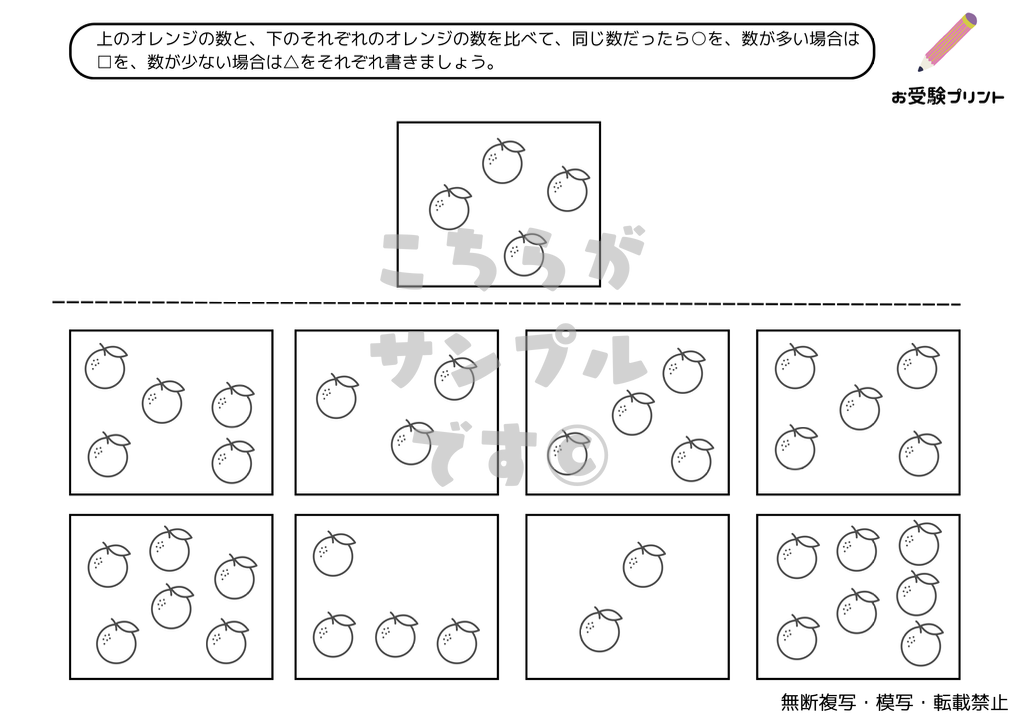
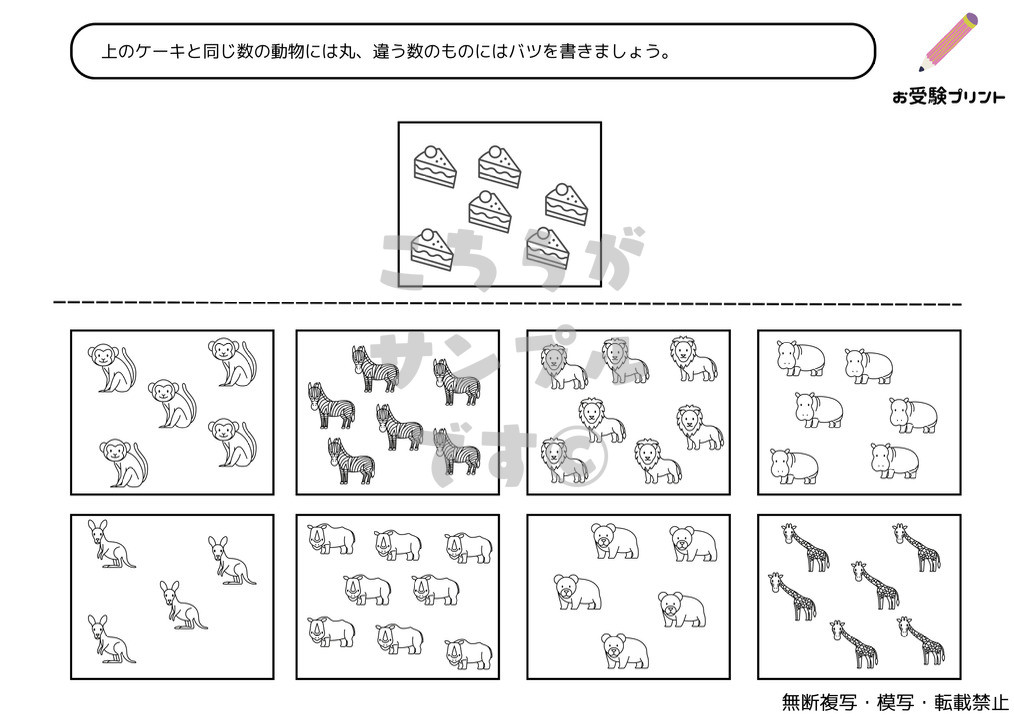
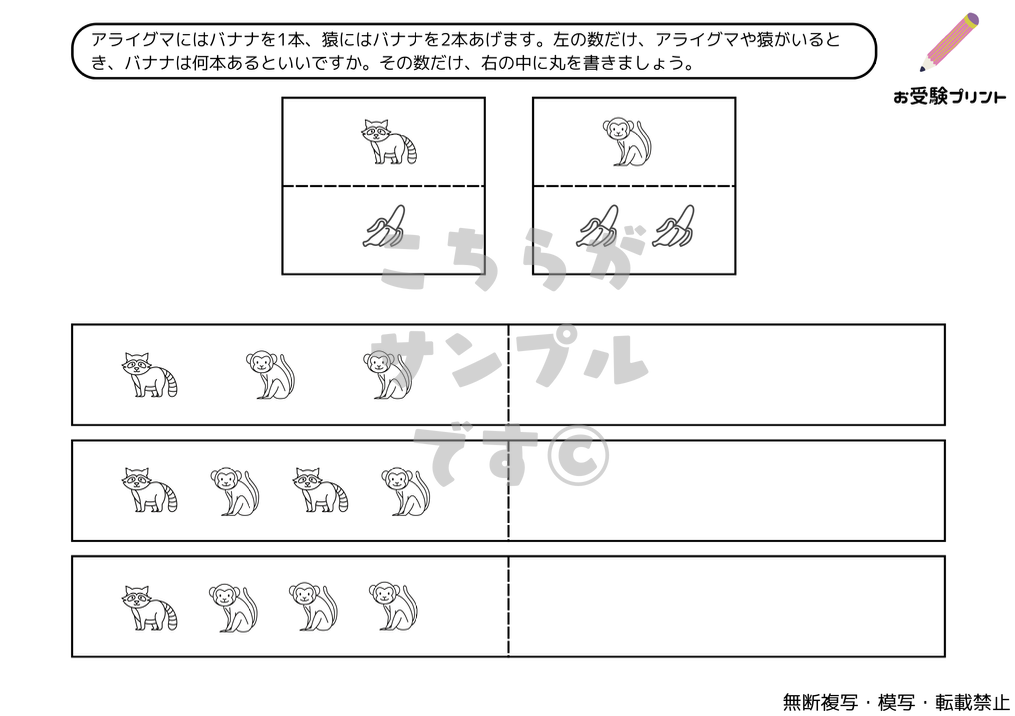
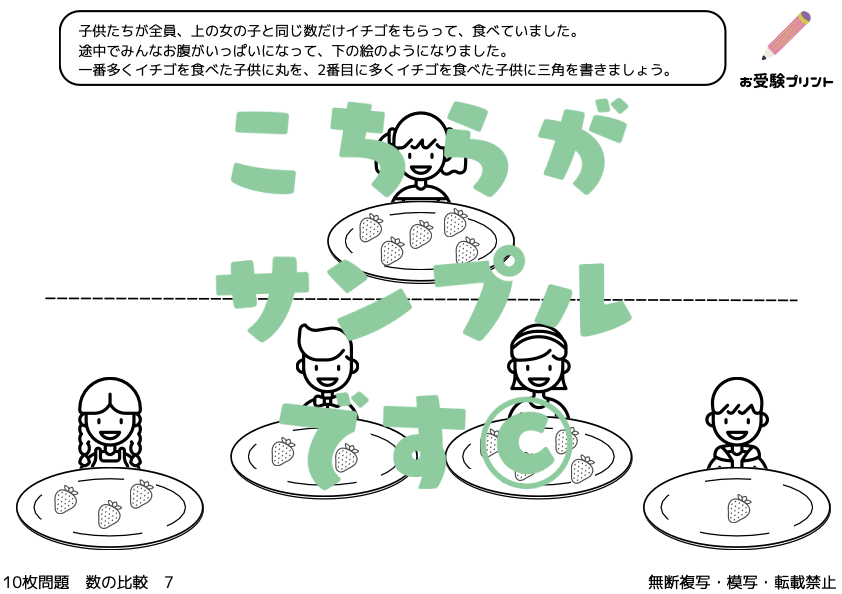
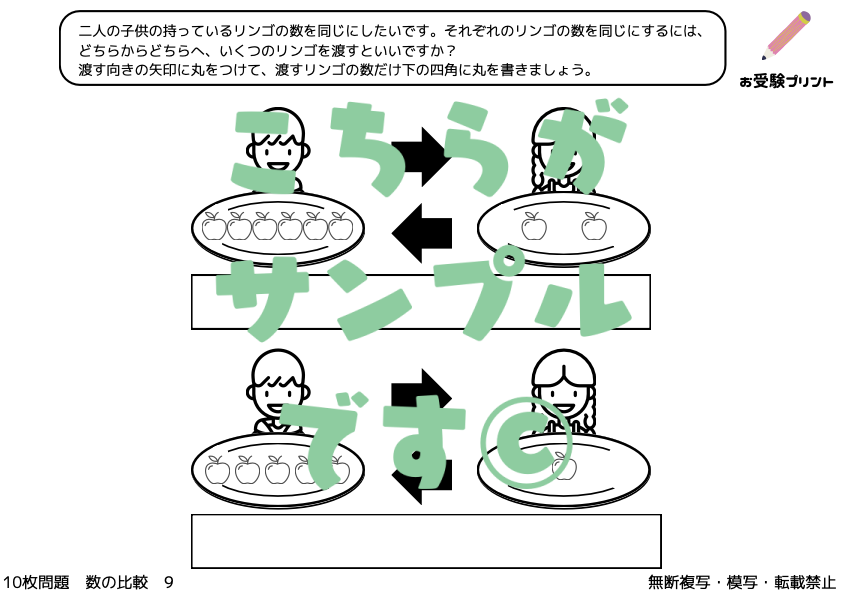
「数の分割・色々な分け方」は、小学校受験の数学の一部として出題される問題です。この問題では、特定の数をいくつかの部分に分ける方法を考えます。例えば、5を分けるとき、5と0、4と1、3と2など、さまざまな組み合わせが考えられます。また、3つ以上に分けることも可能で、5を3つに分けるときは、2と2と1、3と1と1などが考えられます。
この問題を解くためには、数の理解と、数を構成する部分を理解することが重要です。また、さまざまな分け方を考えることで、数の組み合わせやパターンを理解することも可能になります。
この問題は、数の理解を深めるだけでなく、論理的思考や創造的思考を育てるのにも役立ちます。子供たちは、同じ数でも色々な分け方があることを学び、数に対する理解を深める力が養われます。
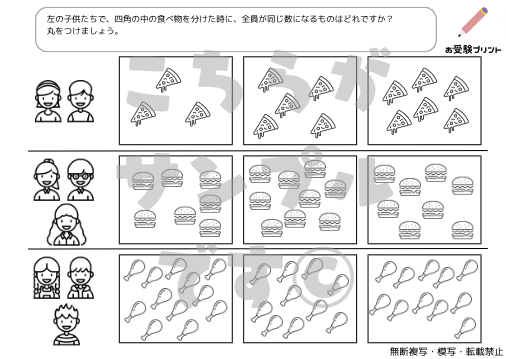
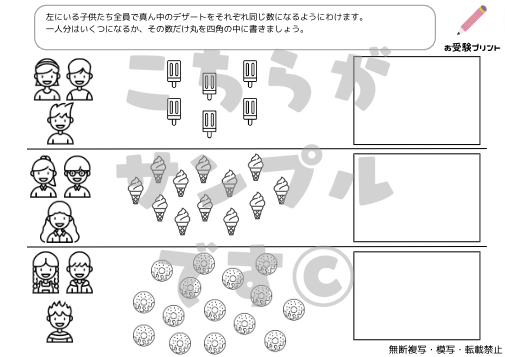
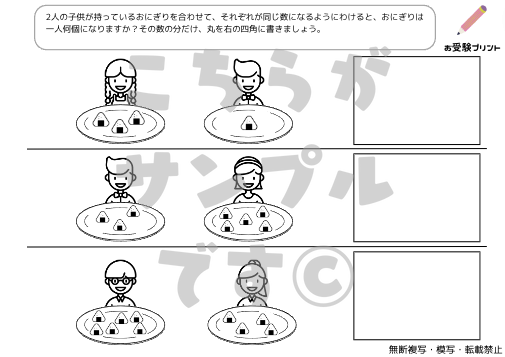
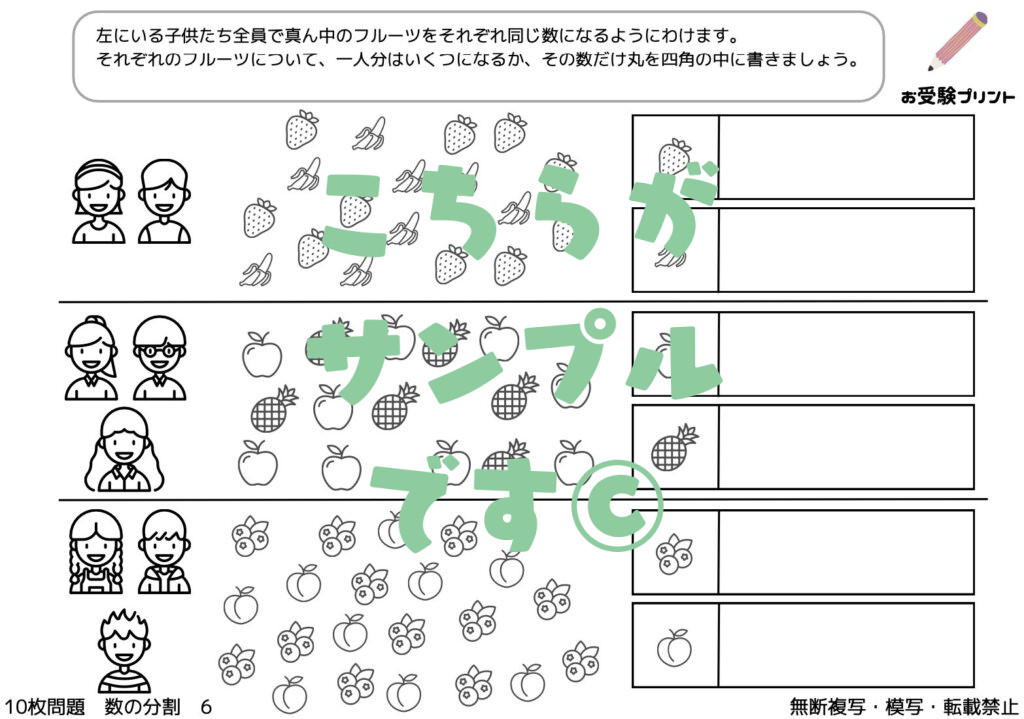
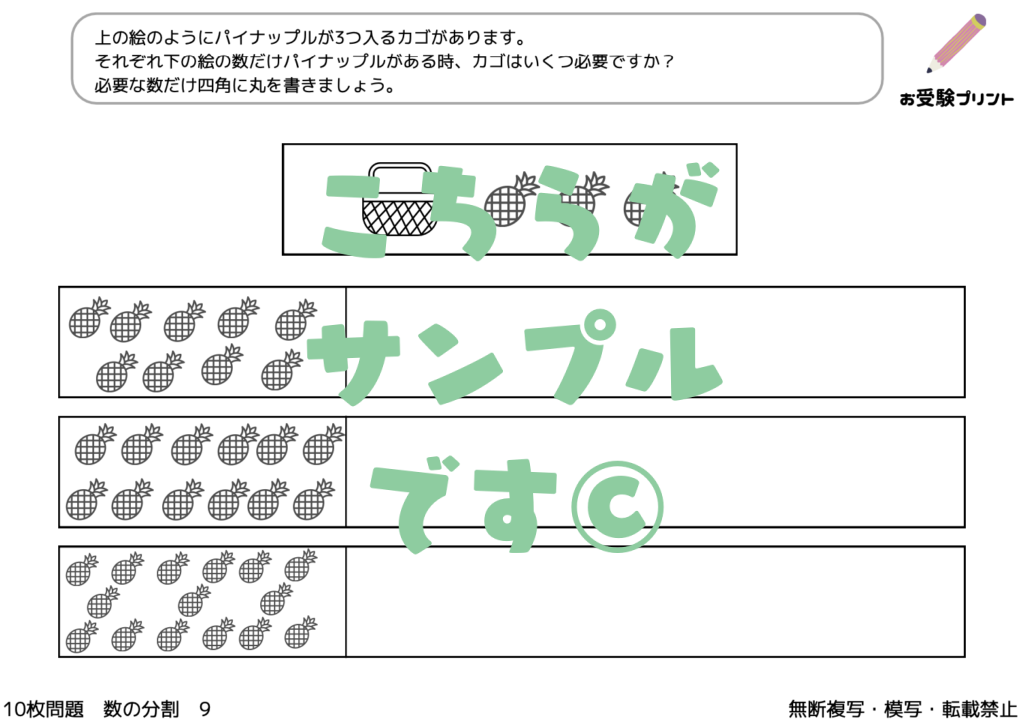
「一対多対応」とは、一つの要素が複数の要素と関連付けられる関係を指します。例えば、一人の先生が複数の生徒を教える、一つの商品が複数のカテゴリーに分類されるなどが該当します。この概念は、小学校受験の算数問題にもしばしば登場します。
例えば、「5人の子供が10個のリンゴを均等に分ける」という問題があったとします。ここで「数の一対多対応」を考えると、一人の子供（一）が2個のリンゴ（多）を受け取る、という関係が成り立ちます。このように、一対多対応の考え方を理解することで、具体的な数の関係を把握しやすくなります。
この概念を理解することは、小学校受験だけでなく、日常生活や他の学習領域においても役立ちます。例えば、一つの原因が複数の結果を生む科学の実験や、一つの出来事が複数の人に影響を及ぼす社会の問題など、様々な場面で「数の一対多対応」の考え方を活用することができます。
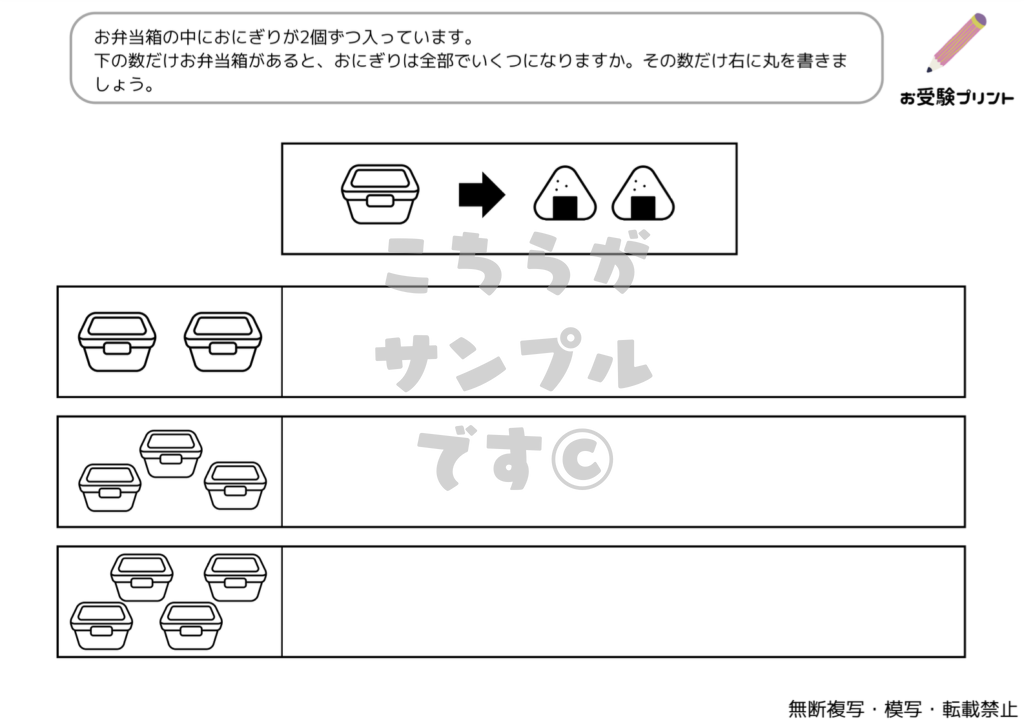
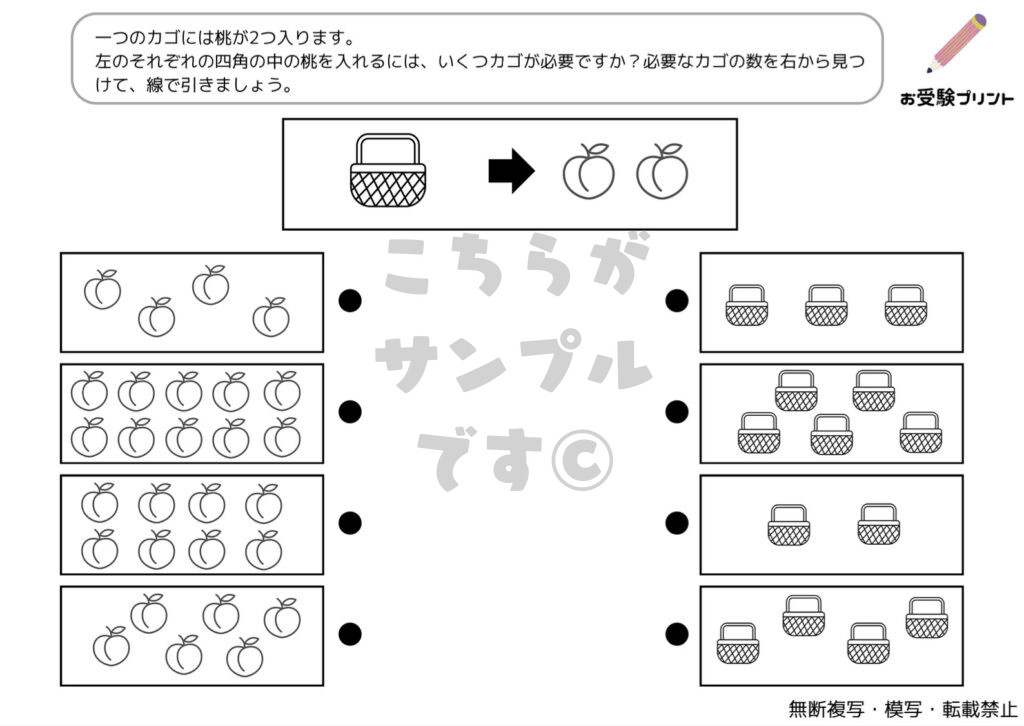
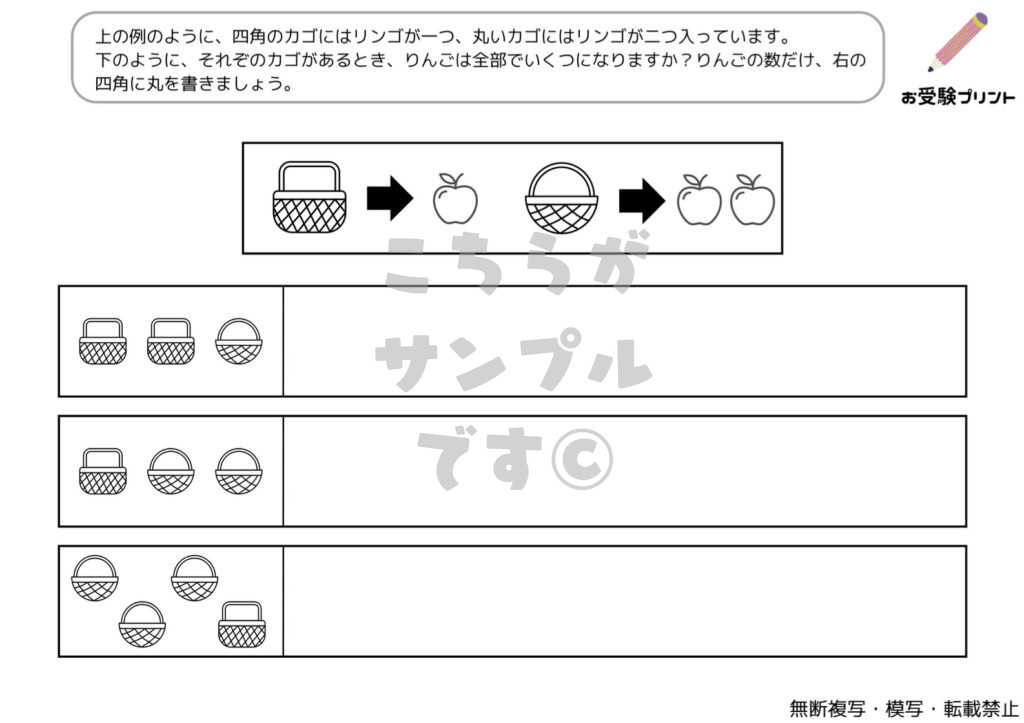
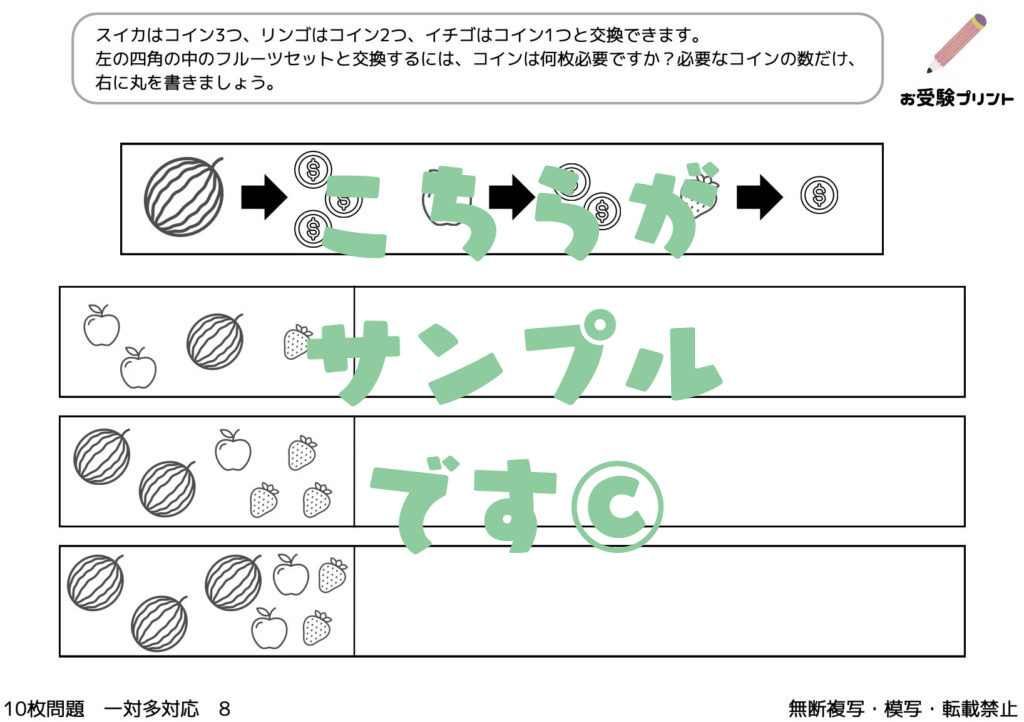
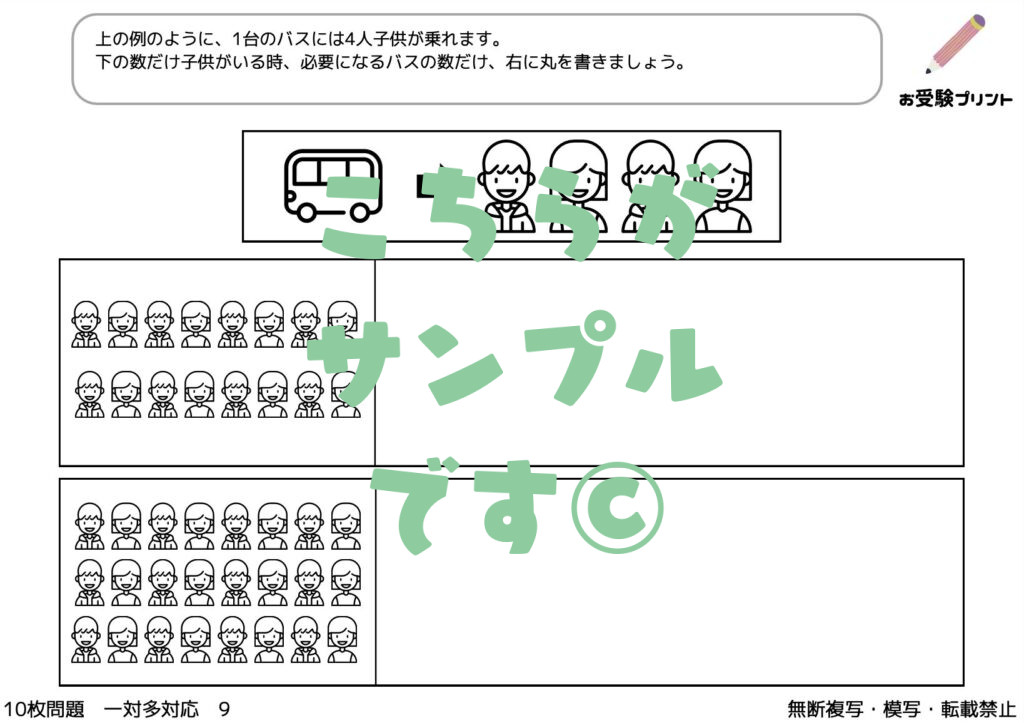
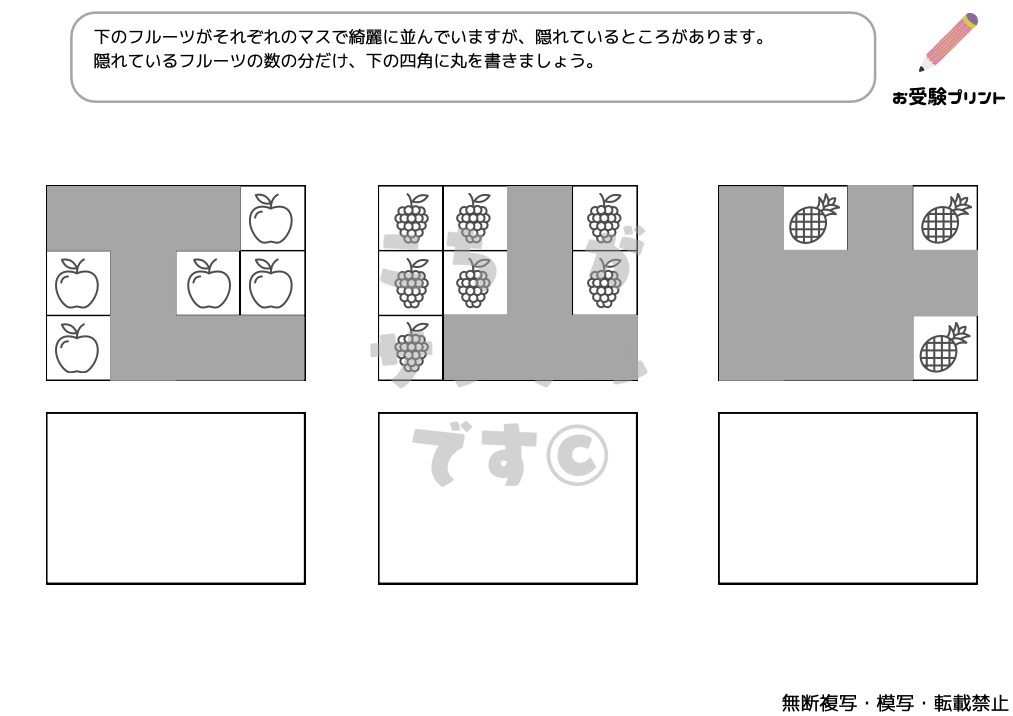
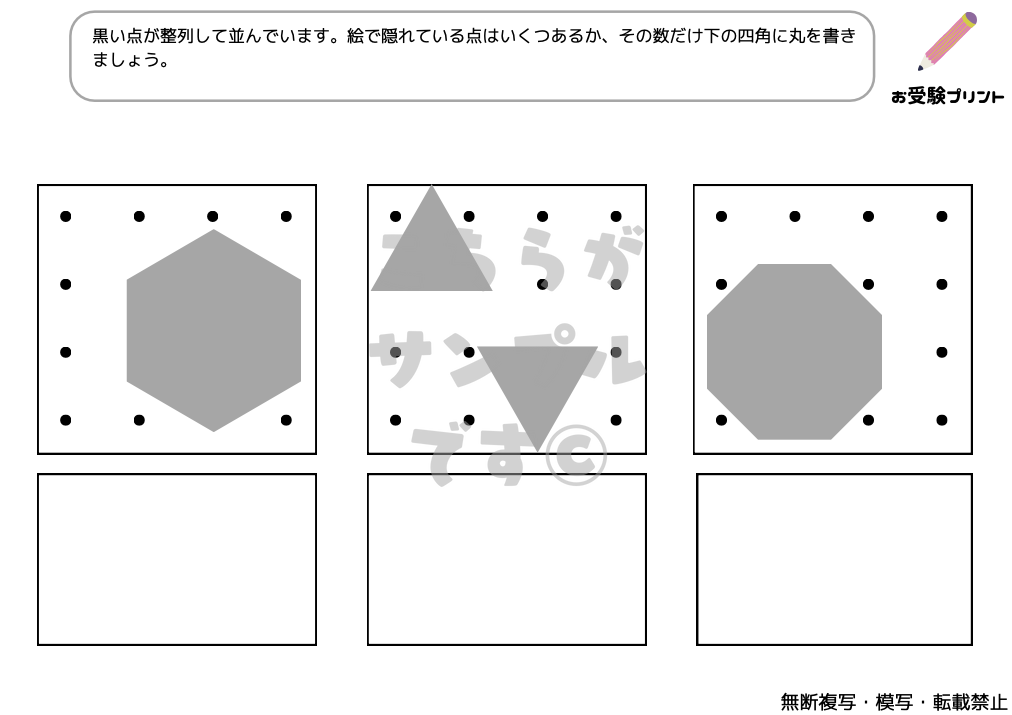
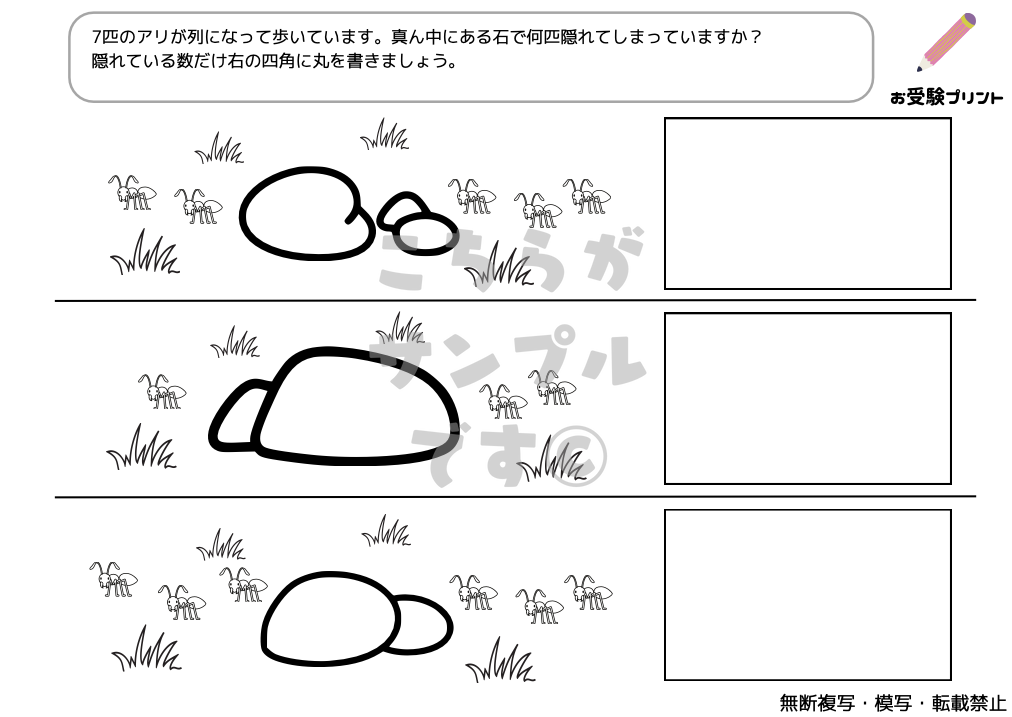
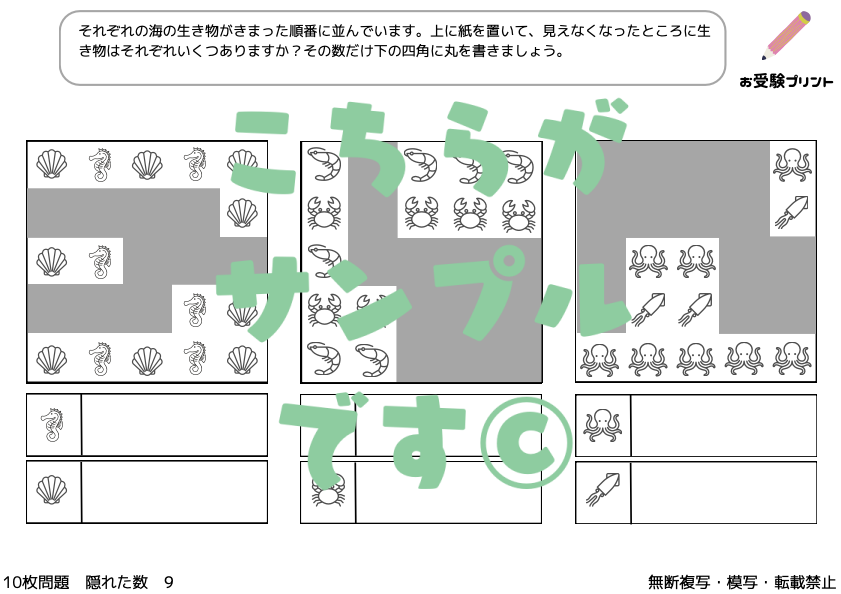
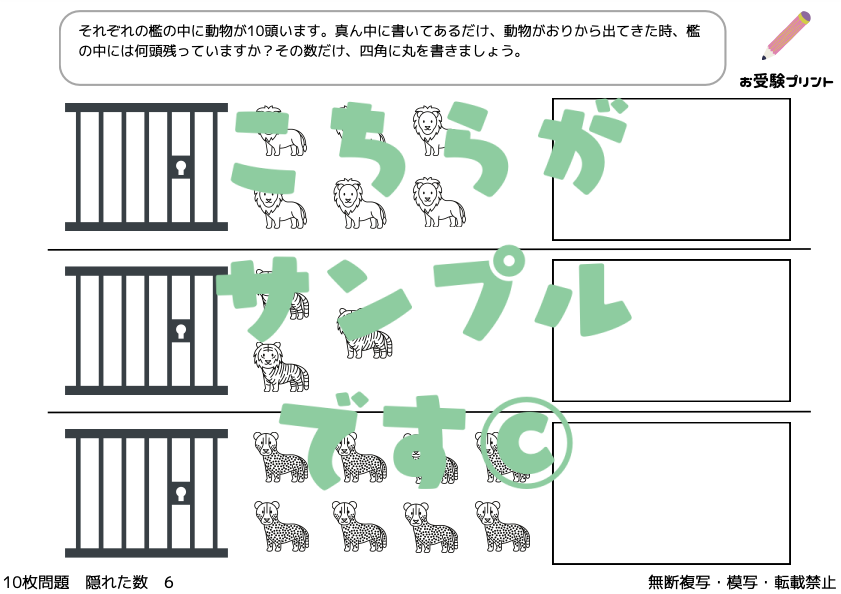
「隠れた数」問題はで、子供たちは、部分的に見えるものの数を基にして、隠れている全体の数を推測する必要があります。例えば、一部が隠されたフルーツや絵カードなどを使用して、全体の数を導き出します。この問題は、単純な記憶や計算を超えた能力が求められます。
子供たちは、見える情報を元にして、隠れた情報を論理的に推測する力を養う必要があります。これには、観察力、推理力、そして数的感覚が必要です。また、この種の問題は、子供たちに数学の基本概念を自然に理解させるのにも役立ちます。「隠れた数」問題は、子供たちに複数のスキルを同時に鍛える機会となります。
問題の形式は様々で、簡単なものから始まり、徐々に複雑さを増していきます。子供たちは、このプロセスを通じて、数の概念をより深く理解し、論理的な思考力を養うことができます。
推理問題は、子供たちが論理的思考を鍛えるための問題です。その解き方は一見すると難しく見えるかもしれません。ここでは、基本的な論理推理から図形を用いた推理まで、さまざまな推理問題の攻略法を解説します。
また、規則性を見つける問題は、子供たちが論理的思考力を鍛えるための重要なステップです。これは、パターンを認識し、それらを理解し、予測する能力を育てます。しかし、子供たちはしばしばパターンの規則性を見つけるのに苦労します。
そのため、教える際には、具体的な例を用いて規則性を明確に示すことが重要です。
複数の条件を組み合わせた推理問題の一つに、「観覧車の問題」があります。これは、観覧車の各ゴンドラに乗っている人々の情報から、特定の条件を満たすゴンドラを推理する問題です。子供が苦労するポイントは、複数の情報を同時に処理することです。教え方のポイントは、まず一つずつ情報を確認し、それを観覧車の模型や図に記入することです。次に、全ての情報を組み合わせて、答えを導き出す練習をさせることが有効です。
図形を用いた推理の一つに、「マジックボックス（魔法の箱）」があります。これは、一部が見えない図形の全体を推理する問題です。子供が苦労するポイントは、見えない部分を想像することです。教え方のポイントは、まず見える部分から推理を始め、次に見えない部分がどのようになっているかを考えさせることです。また、実際に紙を折ったり、カードを回転させたりして、図形の変化を体験させることも有効です。
パターン認識は、物事の間に存在する規則性や連続性を見つける能力です。系列問題は、このパターン認識を鍛えるのに適した問題です。系列問題では、一連の数字や図形が与えられ、その中の規則性を見つけ出し、次に来るべき要素を予測することが求められます。子供たちは、初めて系列問題に取り組むとき、規則性を見つけるのに苦労するかもしれません。そのため、教える際には、まずは簡単なパターンから始め、徐々に複雑なパターンに移行することが推奨されます。また、規則性が見つからないときは、一歩戻って全体を見直すことを促すことも重要です。
順序と整列の問題では、物事が特定の順序で並べられていることを理解する能力が求められます。また、マス目移動の問題では、特定の規則に従ってマス目を移動する能力が必要となります。これらの問題は、子供たちの空間認識能力と論理的思考力を鍛えます。しかし、子供たちはしばしば、順序や整列の規則性を見つけるのに苦労します。そのため、教える際には、規則性を明確に示し、具体的な例を用いて説明することが重要です。
規則性のある数列の問題では、一連の数字が特定の規則に従って並べられていることを理解する能力が求められます。置き換えの問題では、特定の規則に従って一つの要素を別の要素に置き換える能力が必要となります。これらの問題は、子供たちの抽象的思考力と論理的思考力を鍛えます。しかし、子供たちはしばしば、規則性を見つけるのに苦労します。そのため、教える際には、規則性を明確に示し、具体的な例を用いて説明することが重要です。
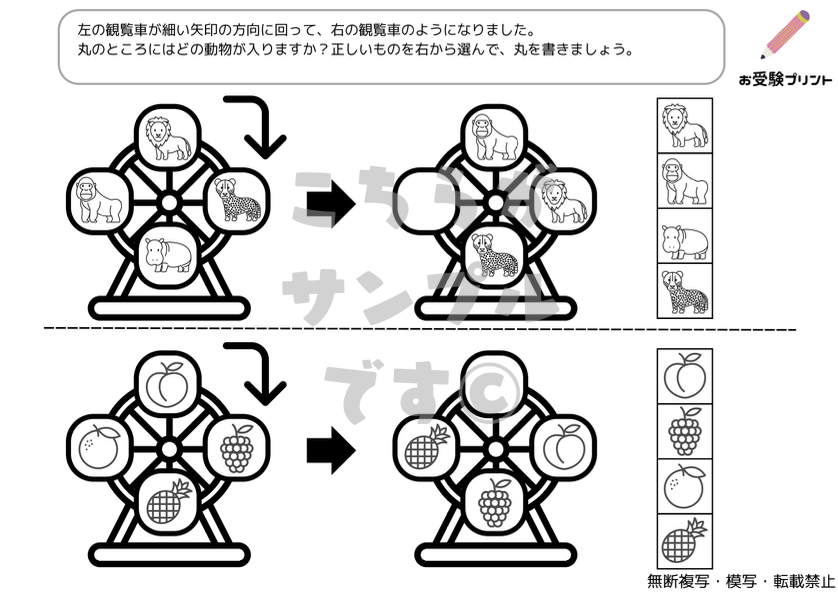
「ルーレット・観覧車」問題は、子供たちの論理的思考力や推理力を試すものです。具体的には、観覧車の各ゴンドラに乗っている人々や物の配置を考える問題で、その配置が変わったときにどのように影響するかを推理する能力が求められます。
例えば、空欄を埋める問題や置換えをして空欄を埋める問題、回転推理などがあります。これらの問題は、子供たちが観覧車の動きを理解し、それに基づいて論理的に考え、答えを導き出す能力を試すものです。
このような問題を解くことで、子供たちは観察力や論理的思考力、空間認識能力を鍛えることができます。また、これらの能力は学業だけでなく、日常生活でも役立つスキルです。
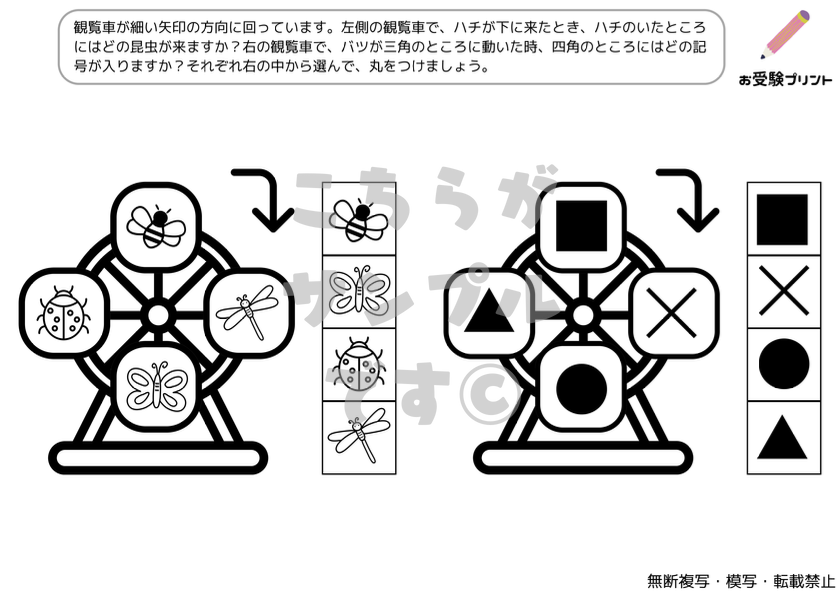
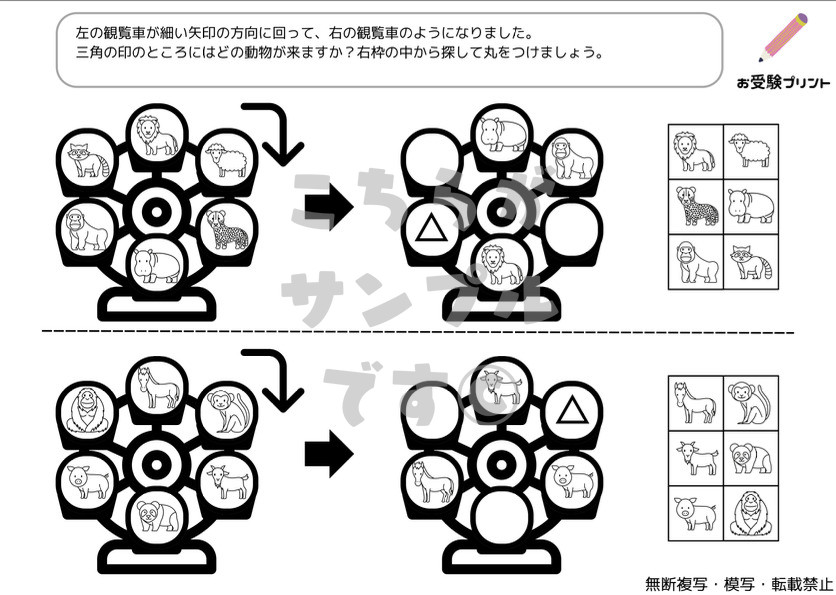
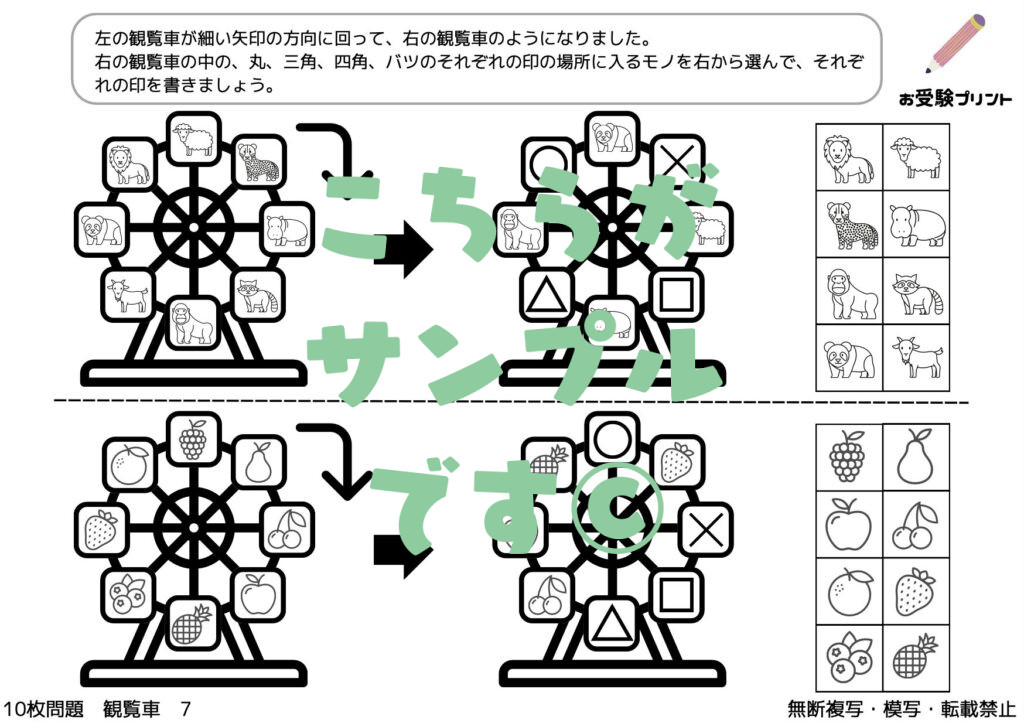
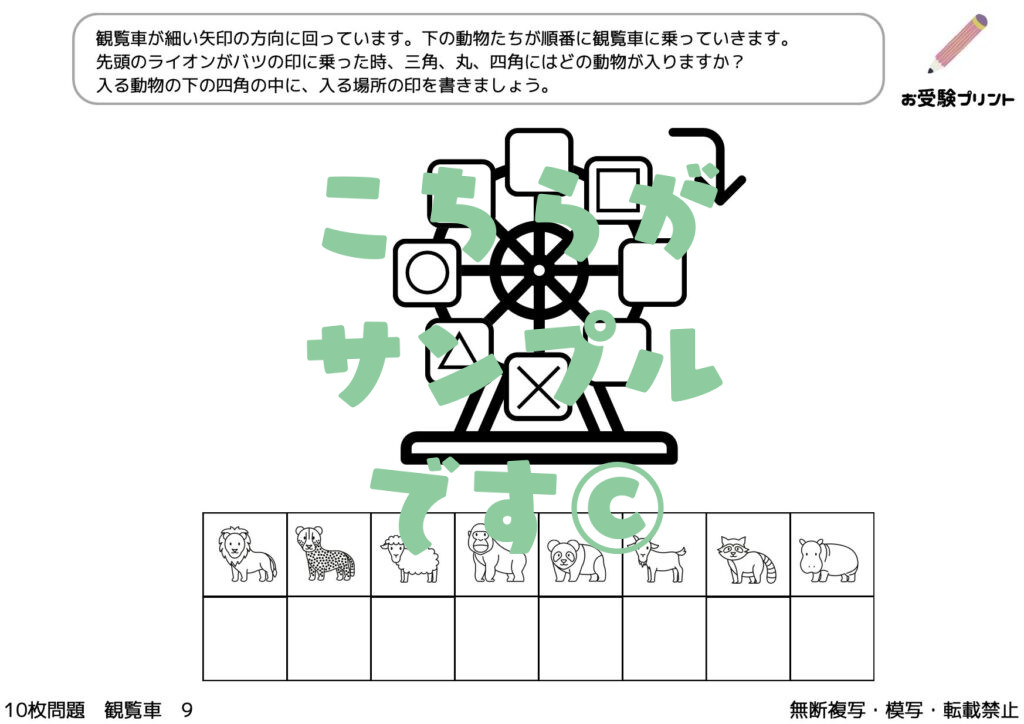
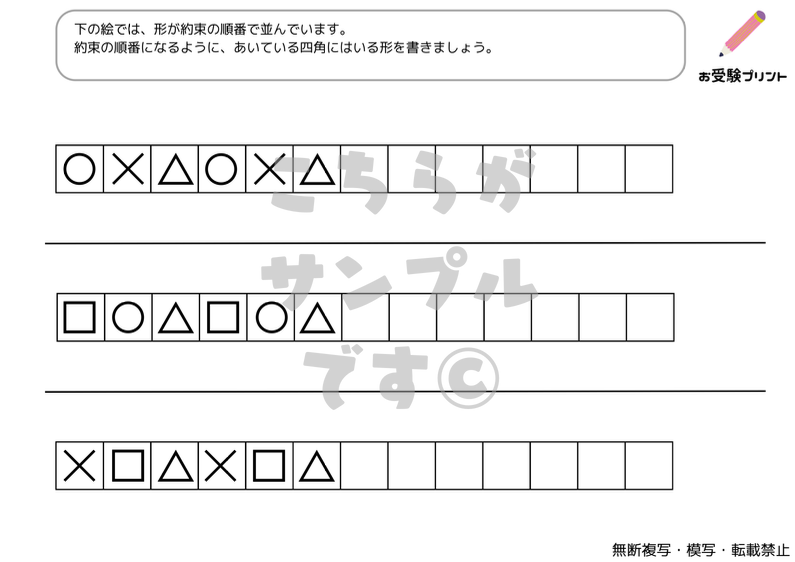
小学校受験における「系列・法則性」の問題は、子供たちがパターンや規則を理解し、それを適用する能力を試すものです。これは、数学的思考や論理的思考を育てるための重要なスキルです。
子供たちは色々な形状やパターンを観察し、それらがどのように連続しているか、または変化しているかを理解することが求められます。また、子供たちは図形の回転や規則性に基づく問題を解く練習が求められます。
これらの問題を解くことで、子供たちはパターンを見つけ、予測を立て、論理的に思考する能力を養います。これは、数学だけでなく、日常生活や他の学問分野においても役立つスキルです。
しかし、これらのスキルを身につけるためには、適切な指導と練習が必要です。そのため、親御さんは、子供が楽しみながら学べるような教材を選び、一緒に学習する時間を持つことが大切です。
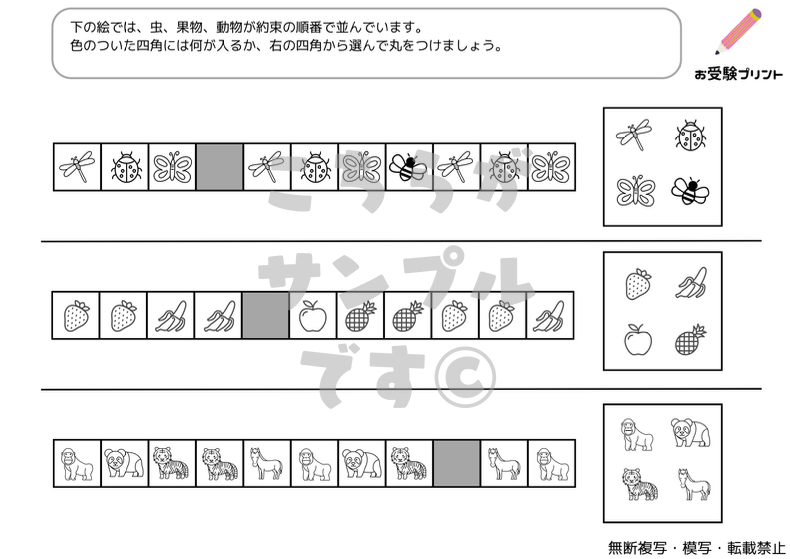
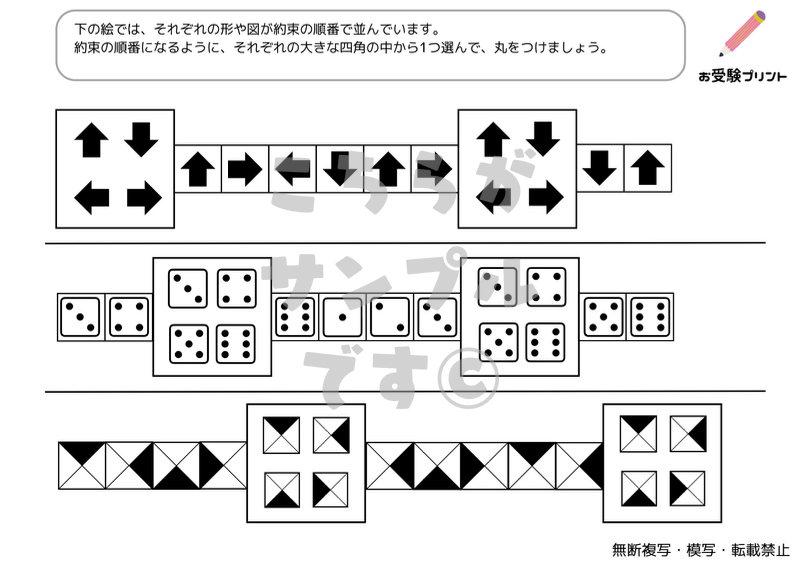
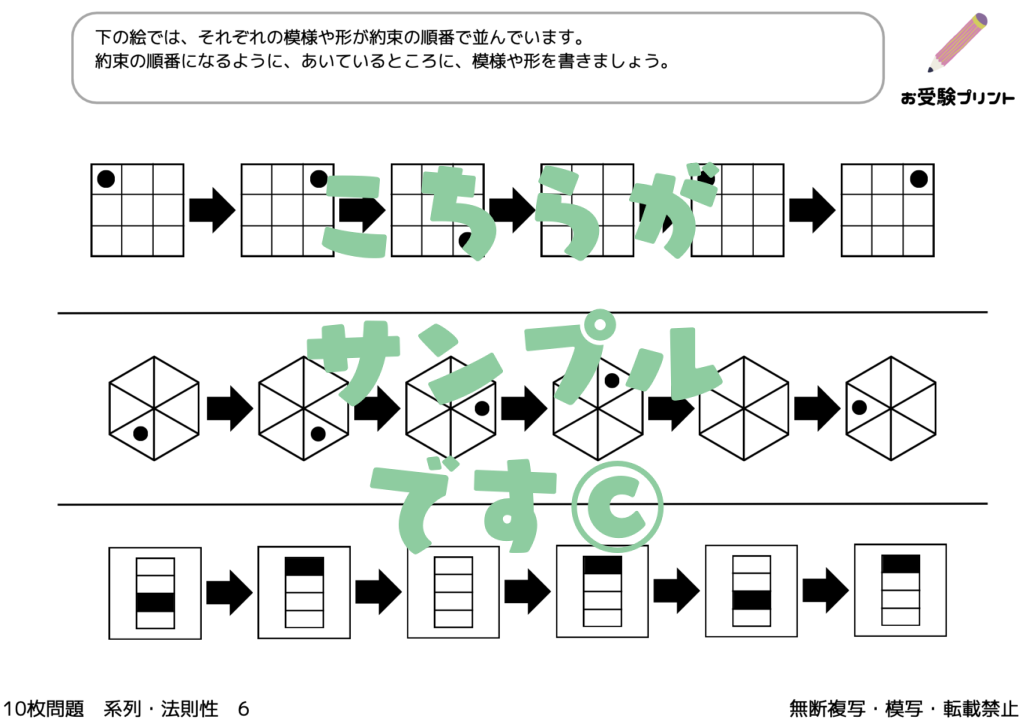
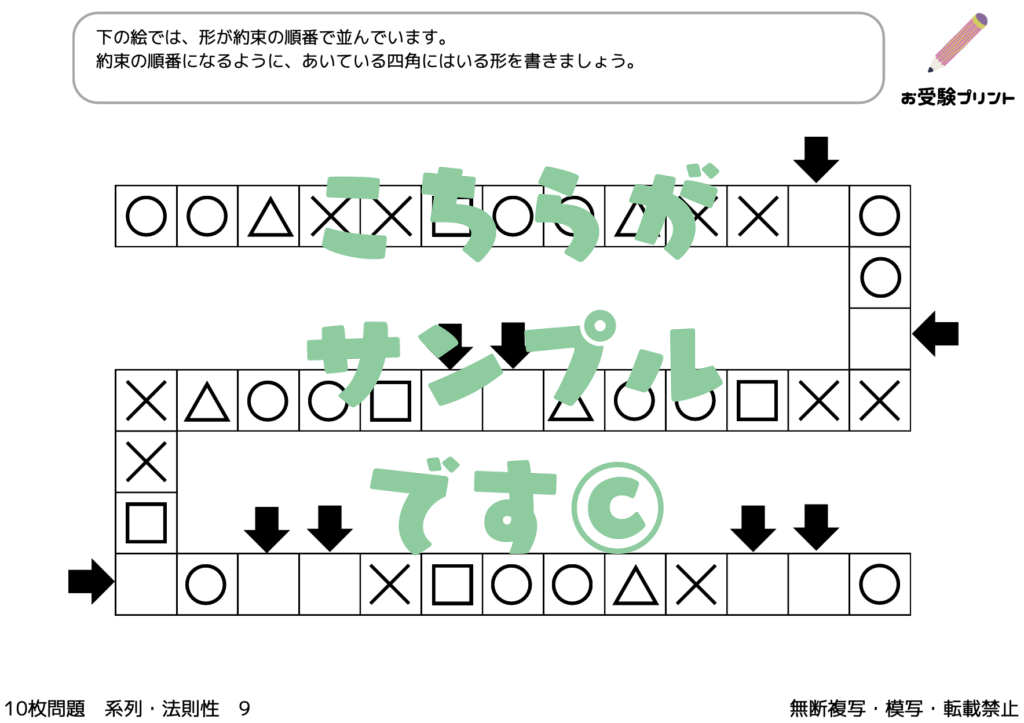
「変化の法則」とは、物事が時間や状況によってどのように変化するかを理解し、予測する能力を指します。これは、小学校受験における重要なスキルの一つであり、特に算数や理科の問題解決に役立ちます。
例えば、図形が一定のルールに従って変化する場合、そのルールを理解し、次にどのような図形になるかを予測することが求められます。また、数列の問題では、数が一定の法則に従って増減するパターンを見つけ出し、次の数を予測することが必要となります。
このように、「変化の法則」は、物事のパターンを理解し、未来を予測するための重要な思考力を育てるものです。これは、学問だけでなく、日常生活や社会生活においても非常に役立つスキルです。
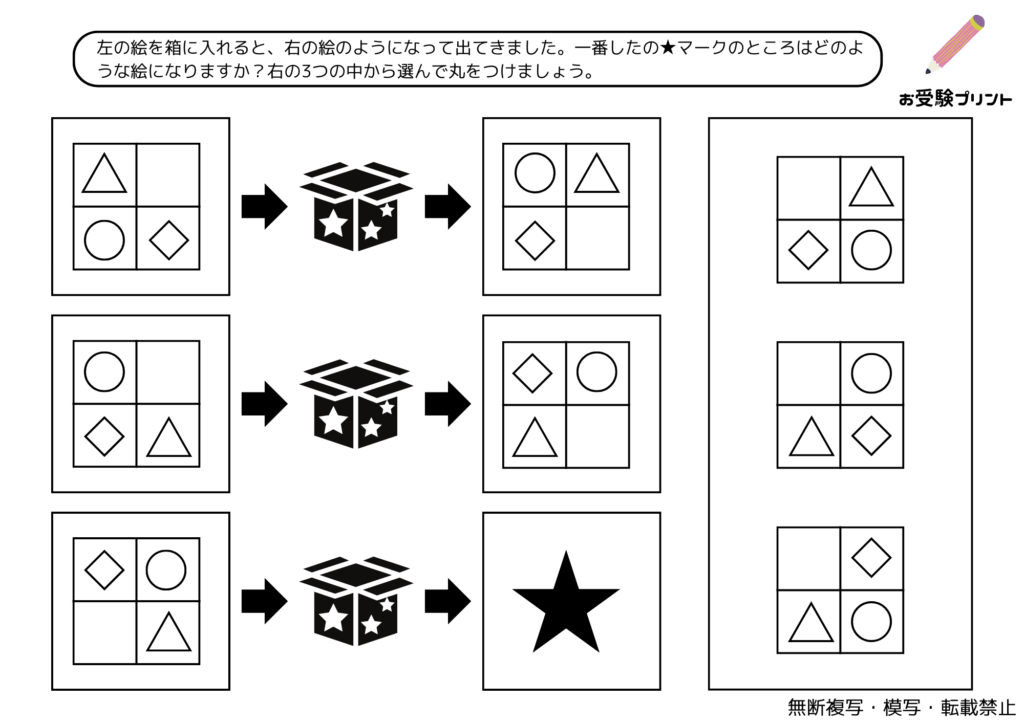
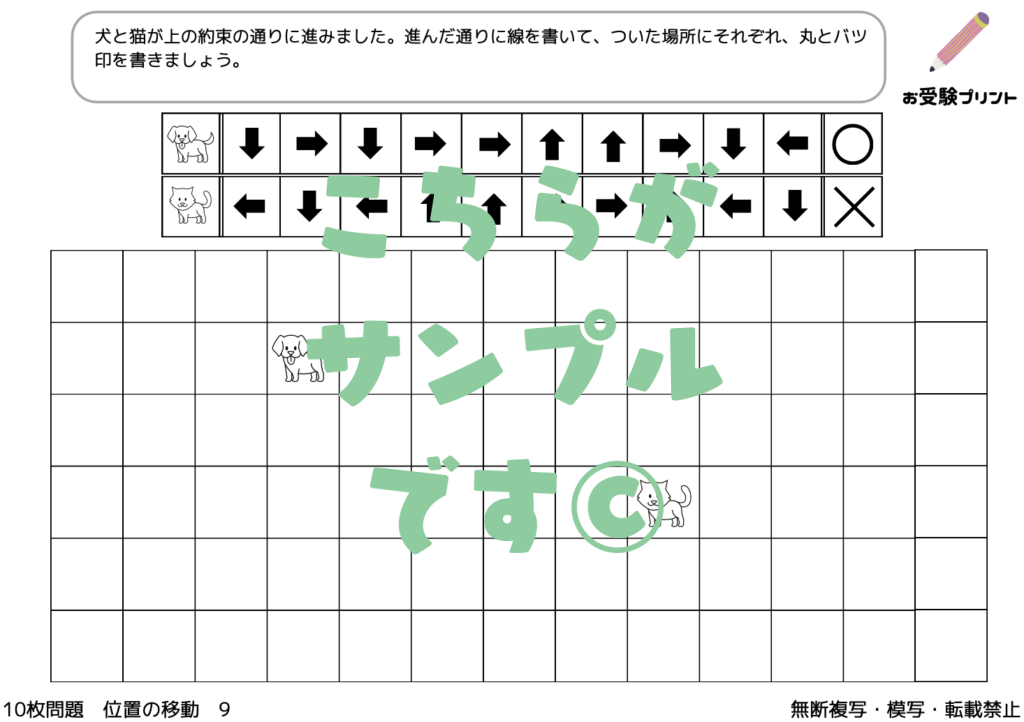
「位置の移動」とは、子供たちが空間認識能力を鍛えるための一種の問題です。これは、物体の位置や方向、移動パターンを理解し、それを適切に表現する能力を育てることを目指しています。例えば、図形の移動や回転、図形の重ね合わせなどが含まれます。
位置問題は、子供たちが物事を視覚的に理解し、その理解を言葉で表現する力を鍛えるのに役立ちます。これは、日常生活だけでなく、学校の学習においても重要なスキルです。また、この種の問題は、子供たちが複雑な問題を解決するための論理的思考力を育てるのにも役立ちます。
位置問題の練習を通じて、子供たちは視覚的な情報を理解し、それを言葉で表現する力を鍛えることができます。これは、将来的に学校の学習や日常生活で役立つ重要なスキルです。
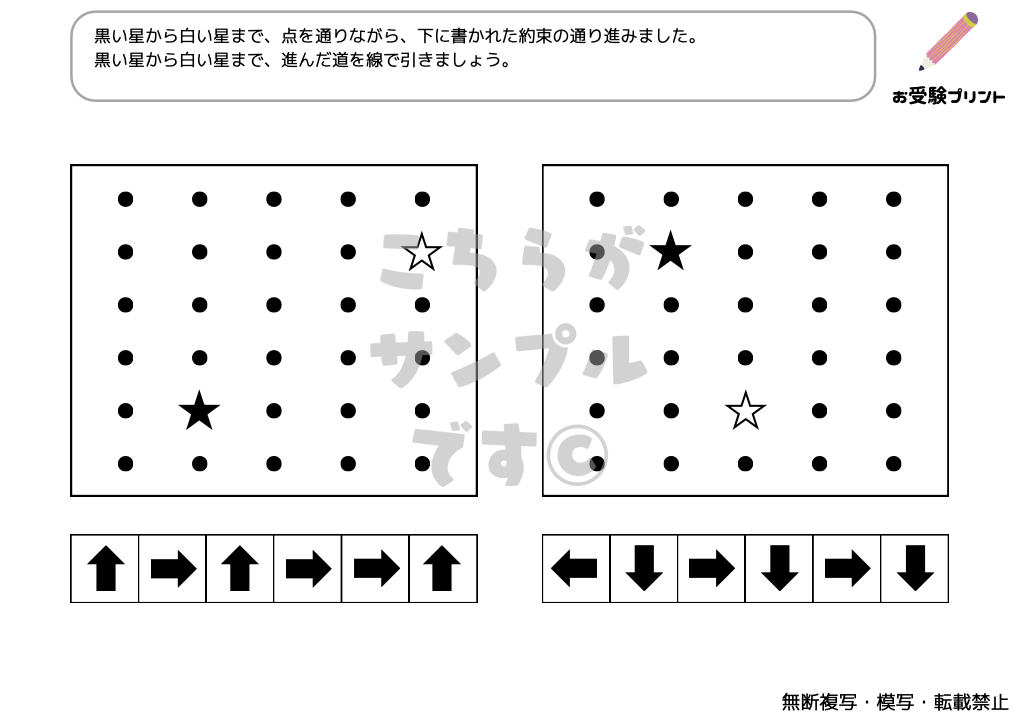
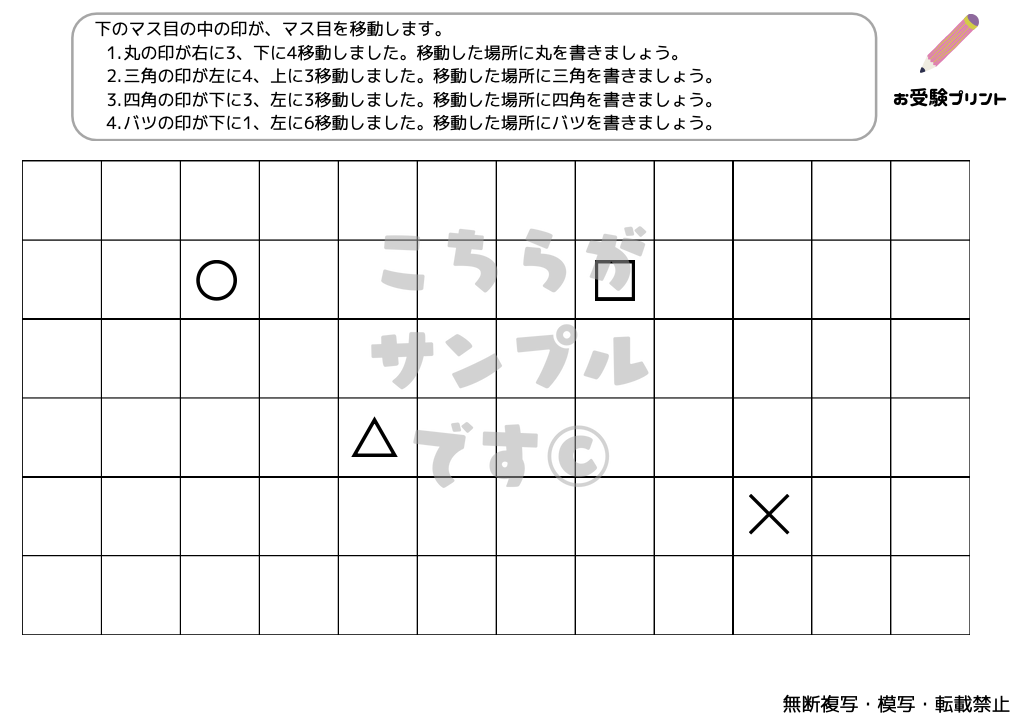
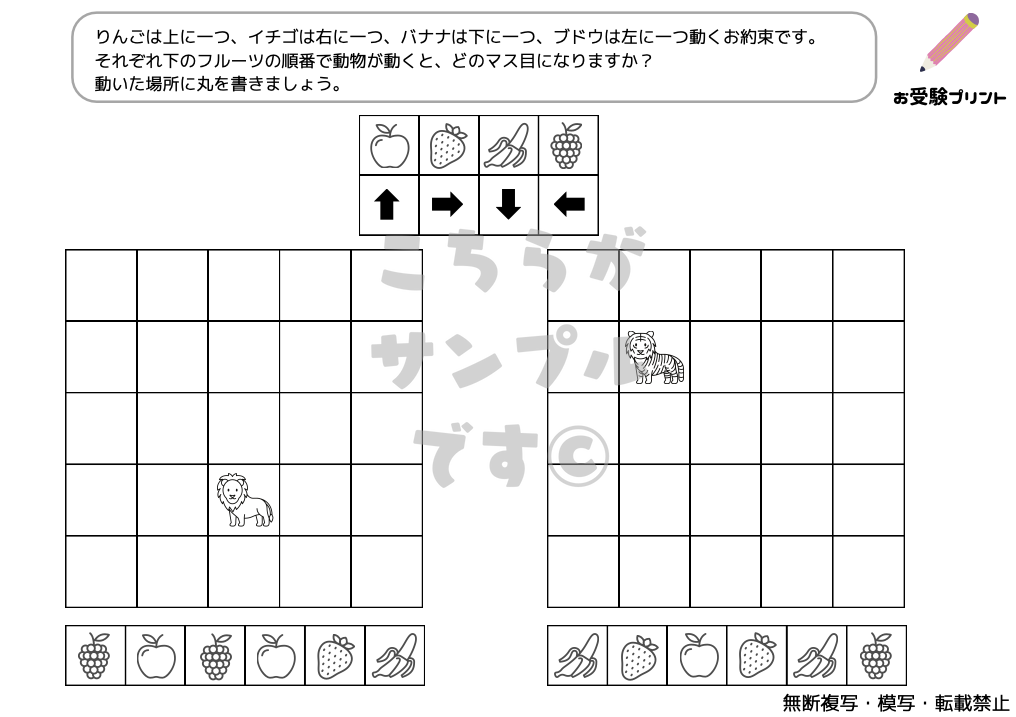
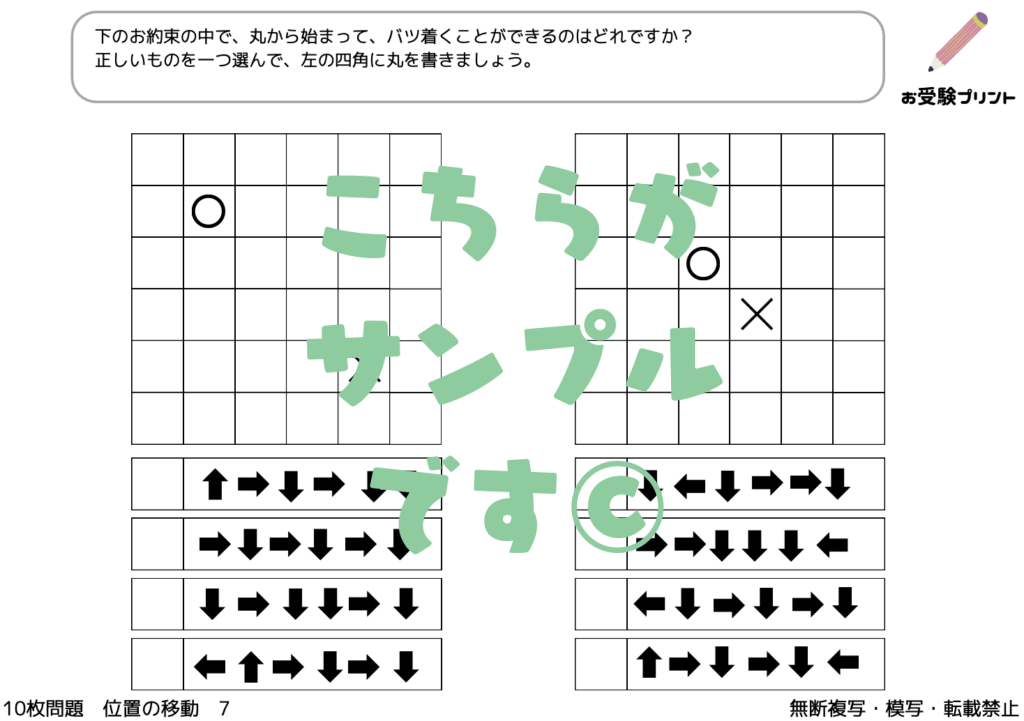
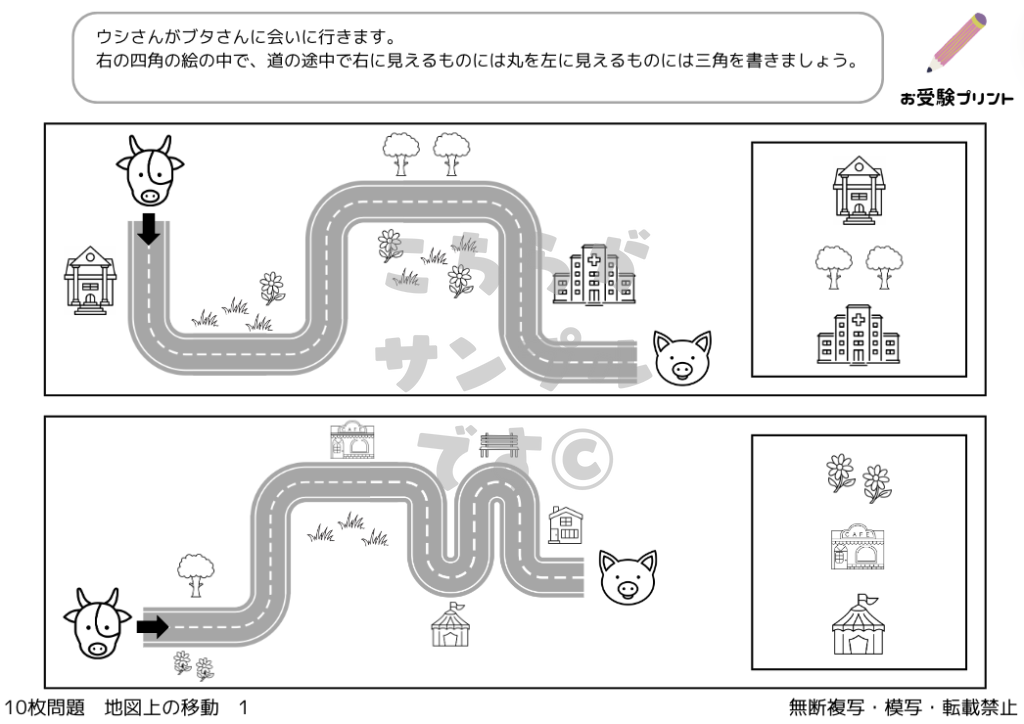
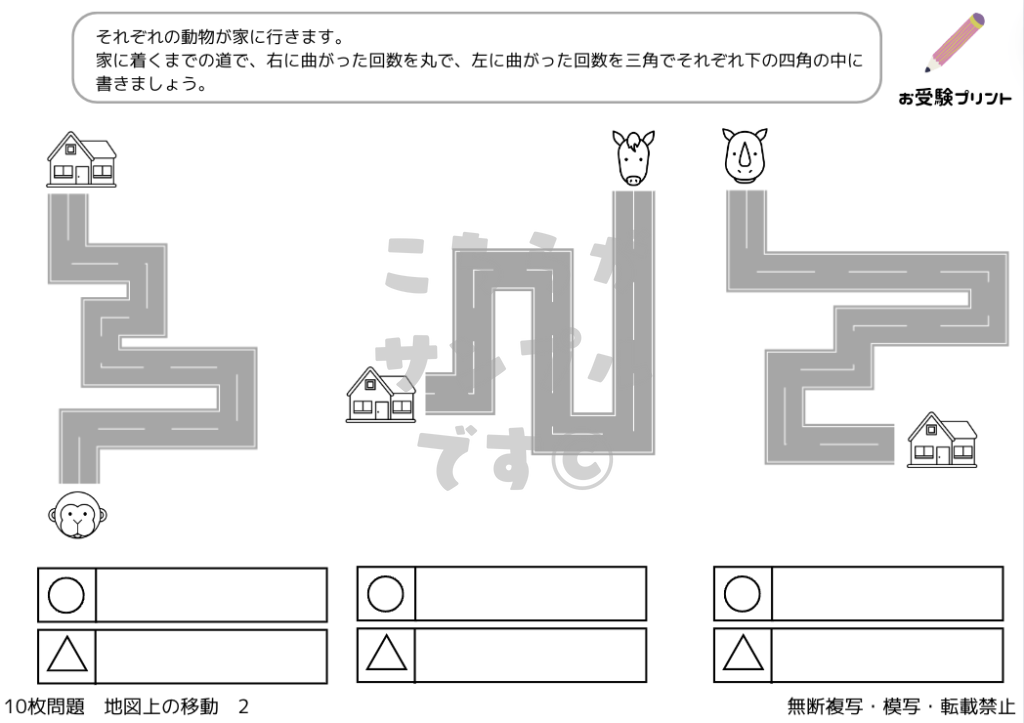
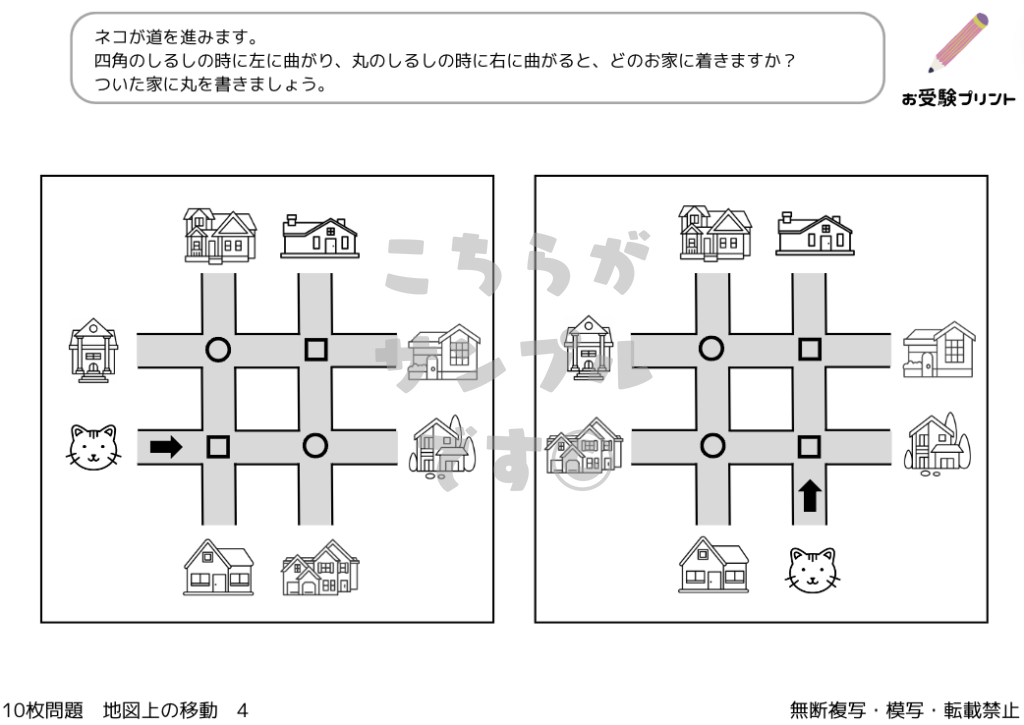
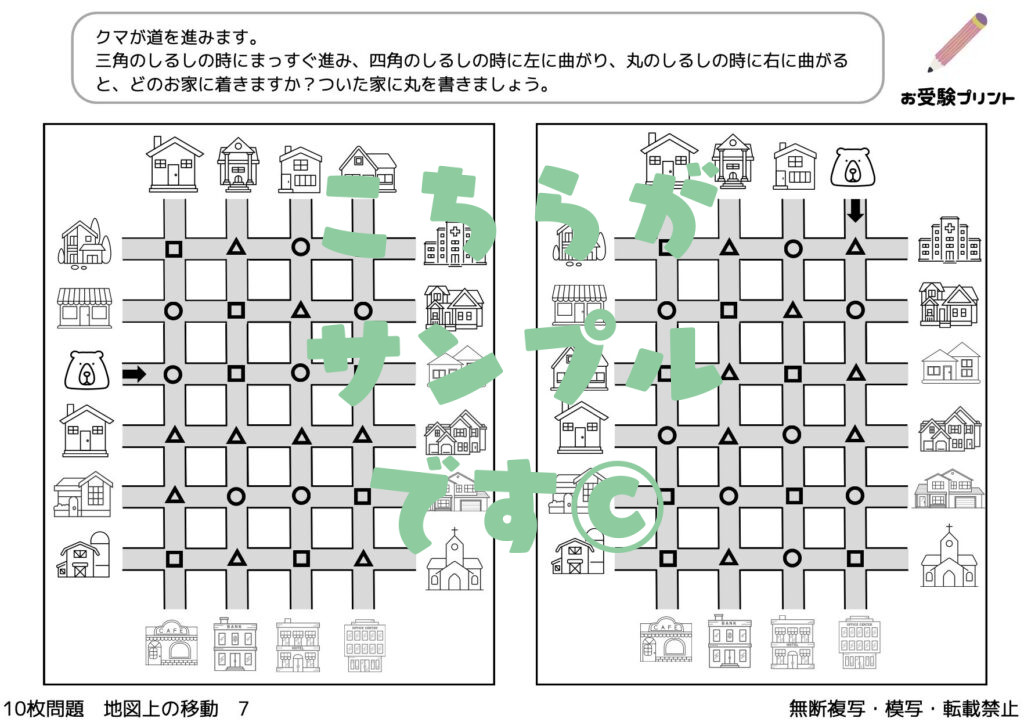
地図上の移動問題は、小学校受験の中で頻出する、子供たちの空間認識能力を試す問題です。具体的には、地図を用いて、指定された地点から別の地点への最適なルートを見つける、または地点間の関係性を理解する問題が含まれます。
この問題は、単なる地理的知識だけでなく、論理的思考や推論能力、さらには注意深い観察力を要求します。地図上の様々な記号や色、線を正しく理解し、それらを実世界の空間と関連付ける能力が必要とされます。さらに、地図上での相対的な位置関係や距離感の理解も重要です。
このように、地図上の移動問題は子供たちに多角的な思考を促し、実際の世界での方向感覚や地図を読むスキルを養う貴重な機会を提供します。
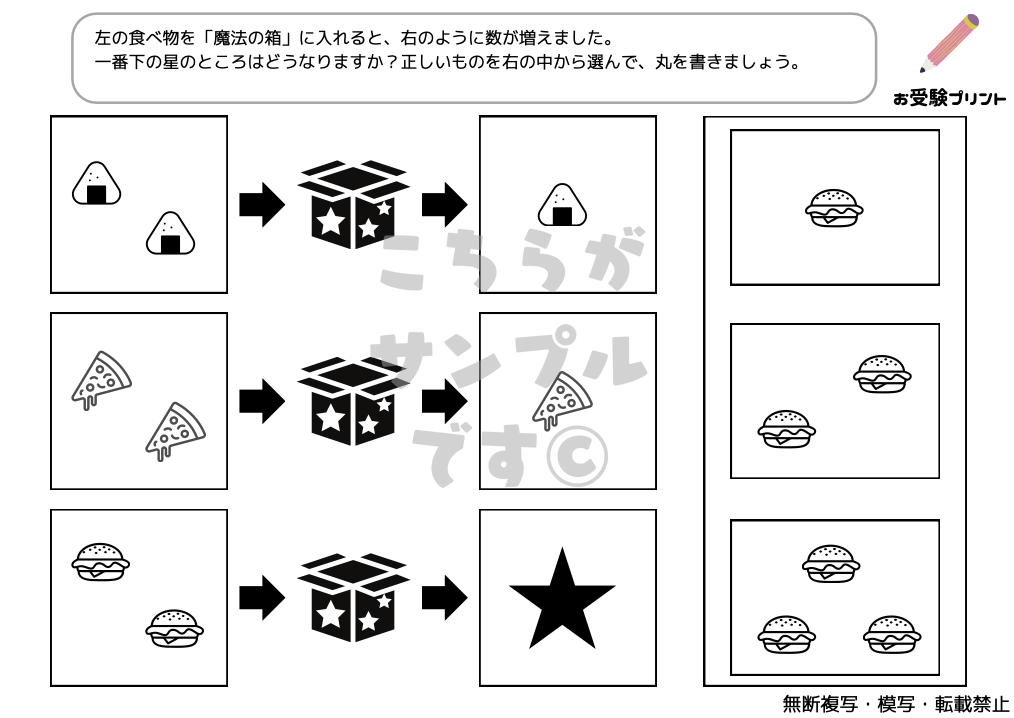
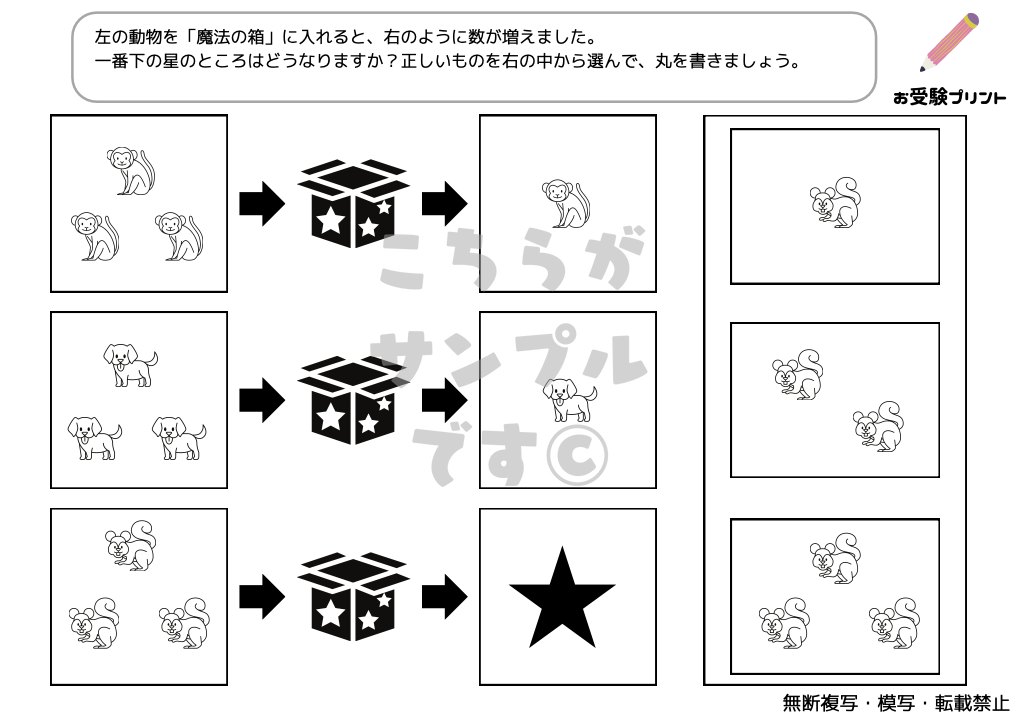
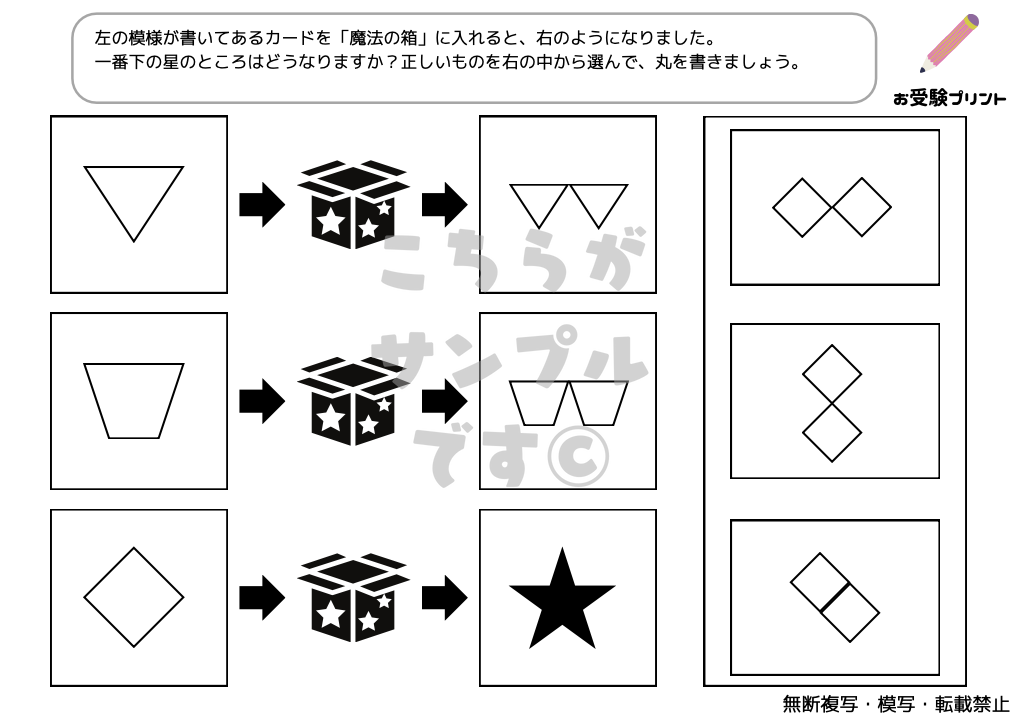
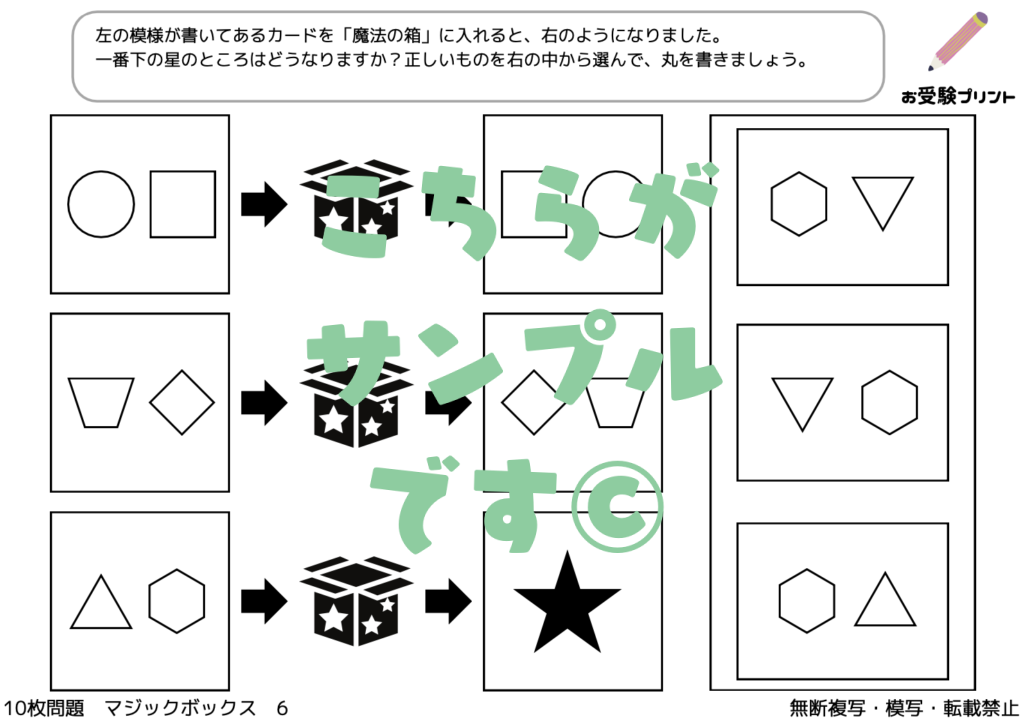
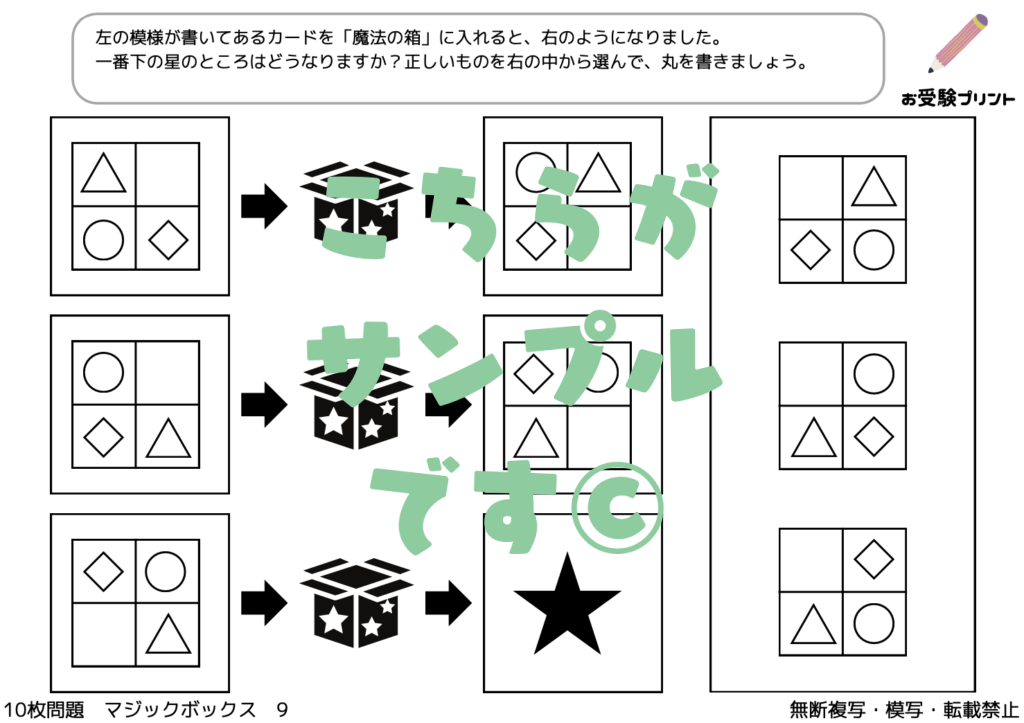
「魔法の箱/マジックボックス」問題は、小学校受験に頻出する論理パズルの一種です。
子供たちは、ある物が「魔法の箱」を通過すると、どのように変化するかを予測することを求められます。
この問題は、子供たちの推理力、注意力、論理的思考力を試すために設計されています。
ルールに基づいて、物が箱を通過する前後でどのように変わるかを理解し、そのパターンを見極めることが求められます。
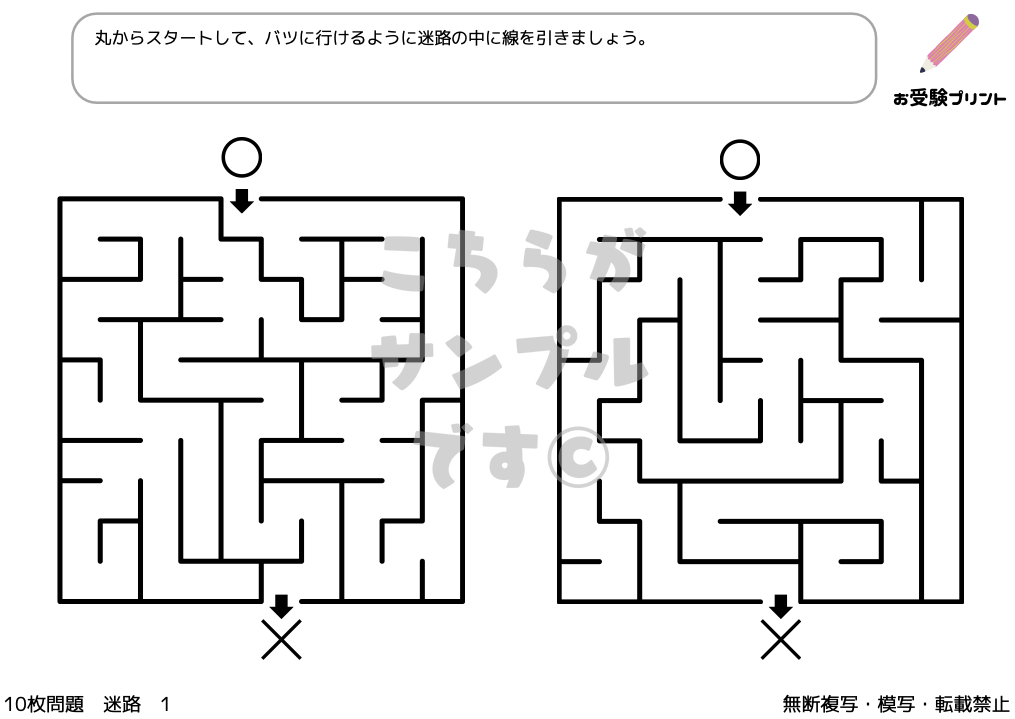
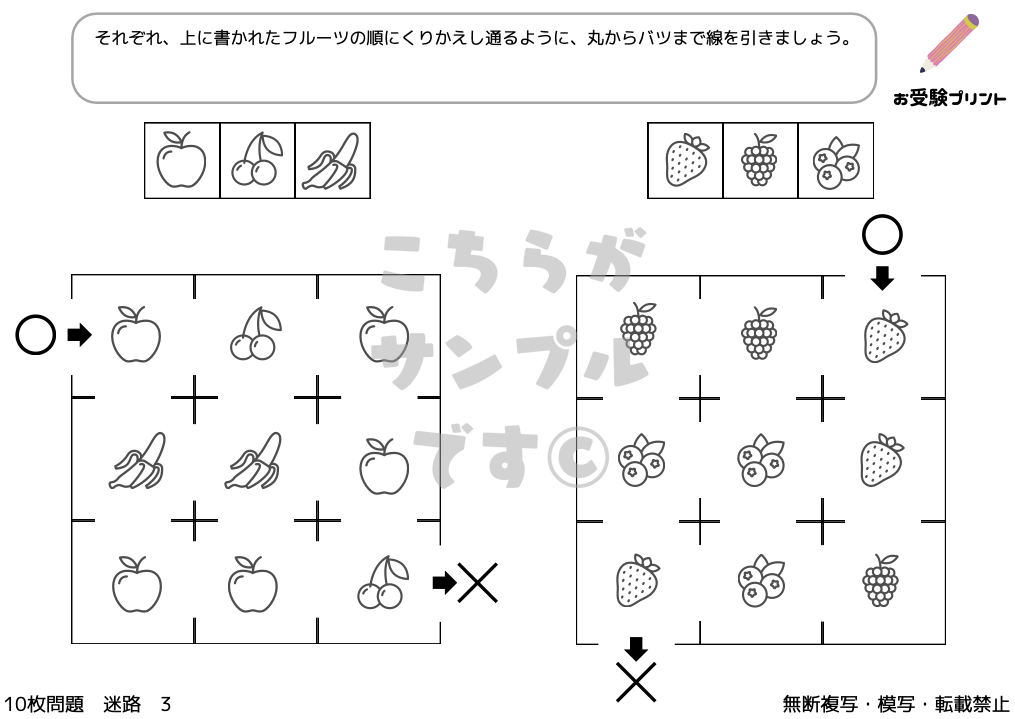
迷路問題は、与えられた迷路を解くことを通じて、子供たちに計画立て、方向性を判断し、状況を分析するスキルを養わせます。迷路問題は単純な道を見つけるだけでなく、条件を満たしながらゴールを目指すものもあり、これにより子供たちは与えられた条件下での意思決定の能力を高めることができます。
たとえば、特定のものがある道を通る、特定の記号を避けるなどの条件が設定されることがあります。このような問題は、子供たちの注意力を高め、一つ一つのステップを慎重に考えるように促します。また、迷路問題は視覚的な知覚と空間認識能力の発達にも役立ちます。
これらの問題を解くことで、子供たちは様々な角度から問題を見る方法を学び、複雑な問題に対する多角的なアプローチを身につけることができます。
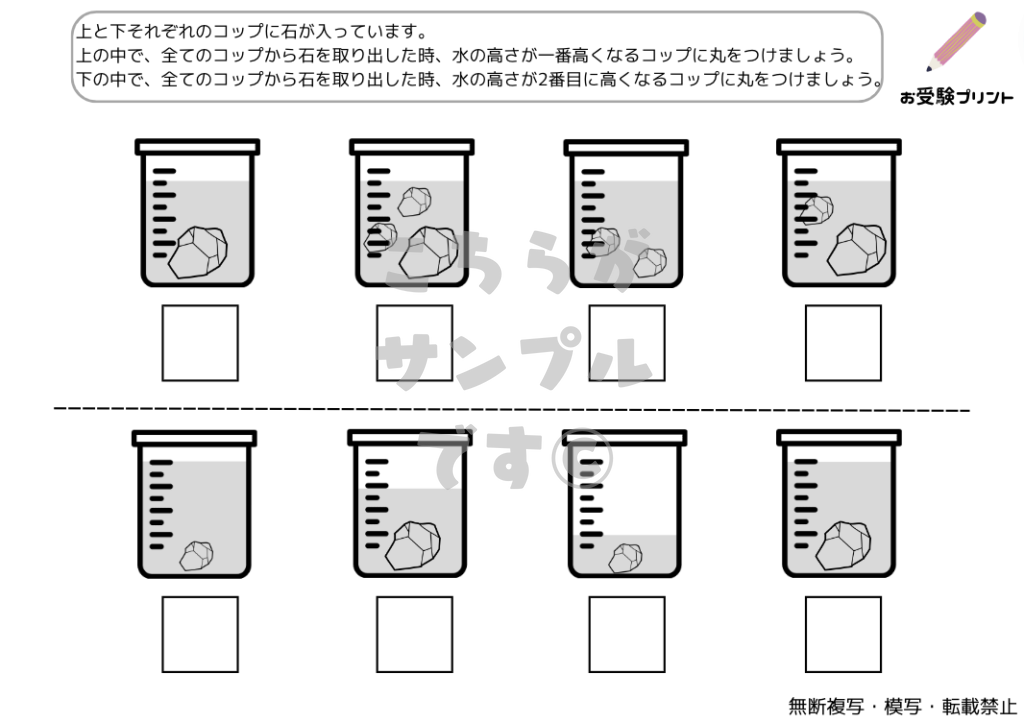
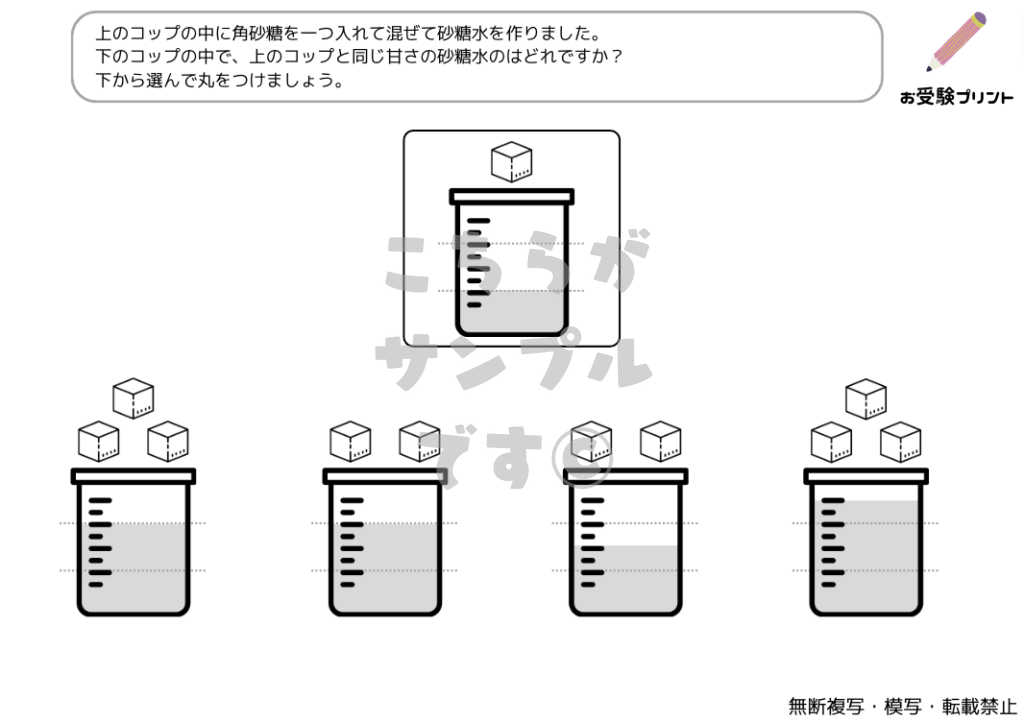
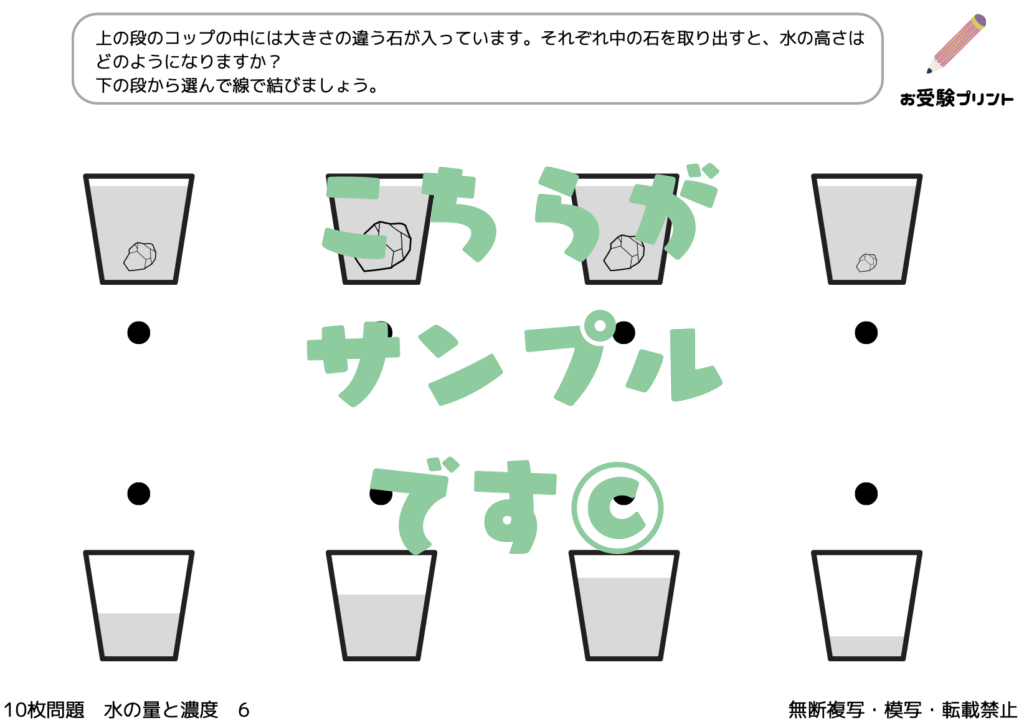
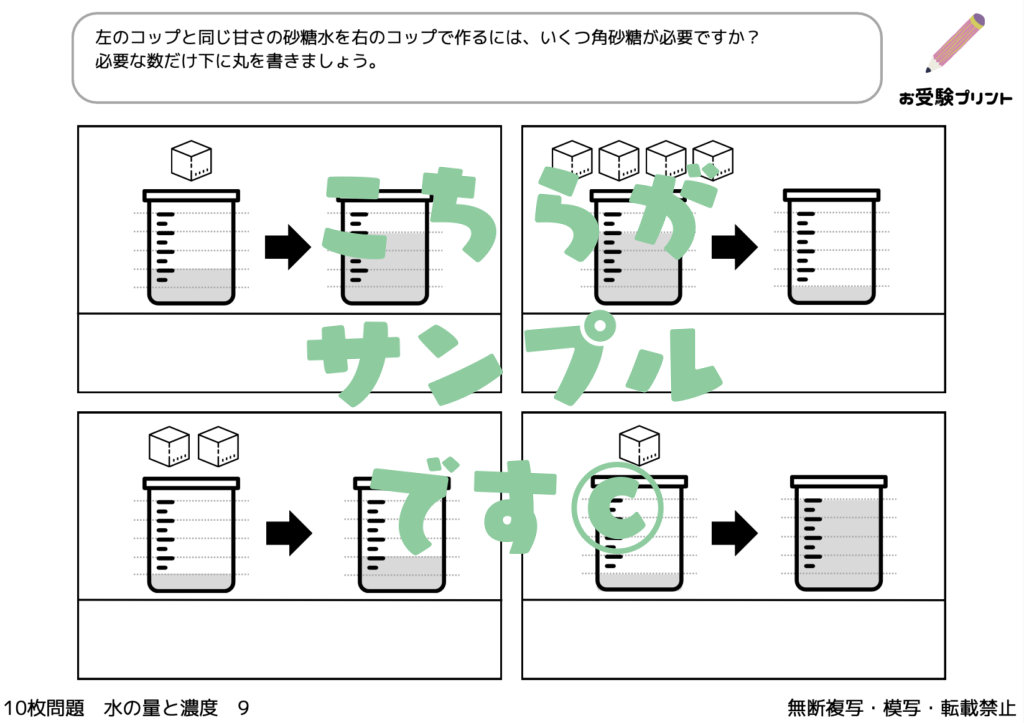
「水の量と濃度」の問題は、小学校受験のペーパー課題の中で頻繁に出題されるテーマの一つです。
具体的には、水や液体の量を比較したり、異なる濃度の液体を比較する問題が出題されます。
これは、子供たちが物の比較や変化を観察する能力を試すものであり、日常生活での経験や学びが非常に重要となります。
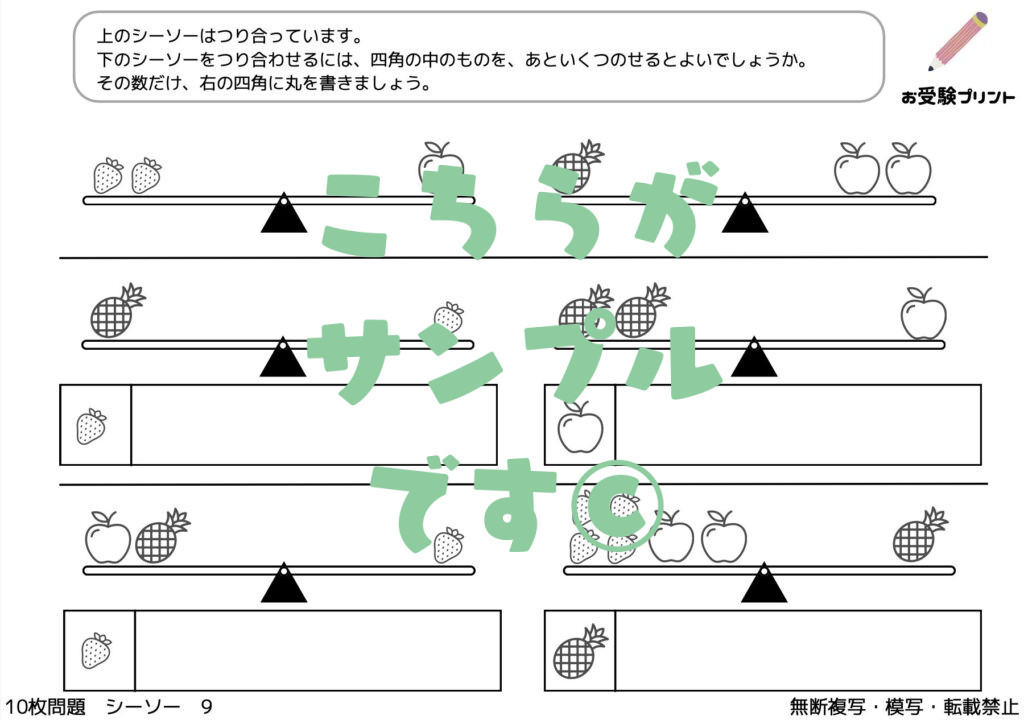
「重さ比べ・シーソー」問題は、小学校受験のテストでよく出題される問題です。
この問題は、シーソーや天秤を用いて複数の物体の重さを比較することを求められます。
子供たちは、シーソーの片側が下がるという現象から、その側が重いと理解し、複数の物体の間でどれが最も重いか、または軽いかを推測する必要があります。
このプロセスを通じて、子供たちは物体間の重量関係を理解し、論理的思考能力を養うことができます。
重要なのは、単に答えを見つけることではなく、その過程で論理的に考え、問題解決する能力を身につけることです。
また、このタイプの問題は、物理的なバランスの概念を理解するのにも役立ち、数学的な思考を促進するのにも有効です。
小学校受験において、この問題は子供たちの分析力と推理力を試すための重要な科目となっています。
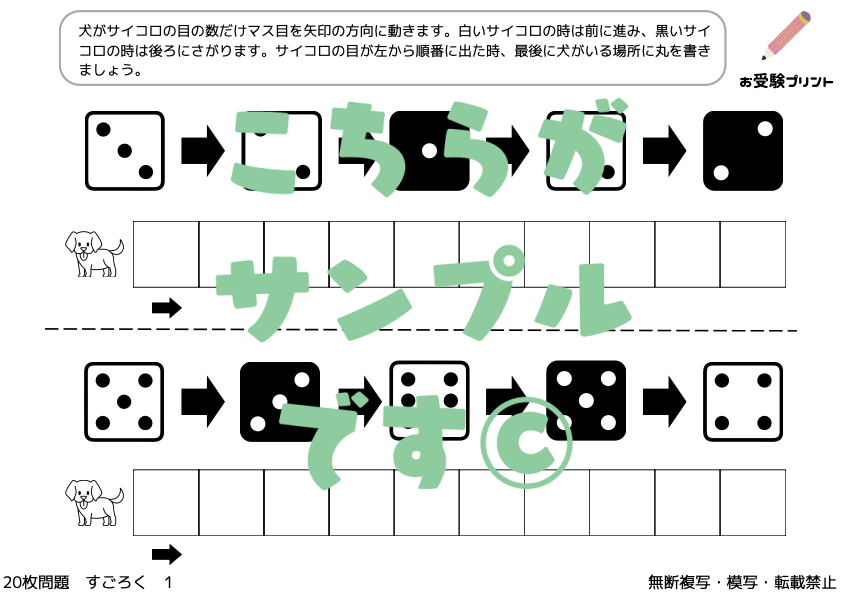
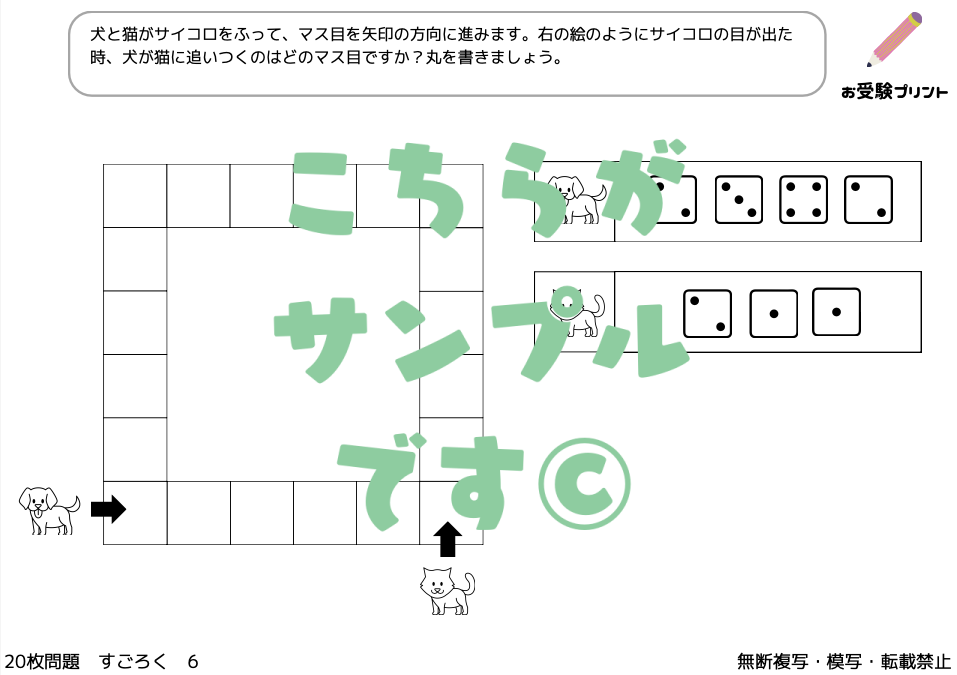
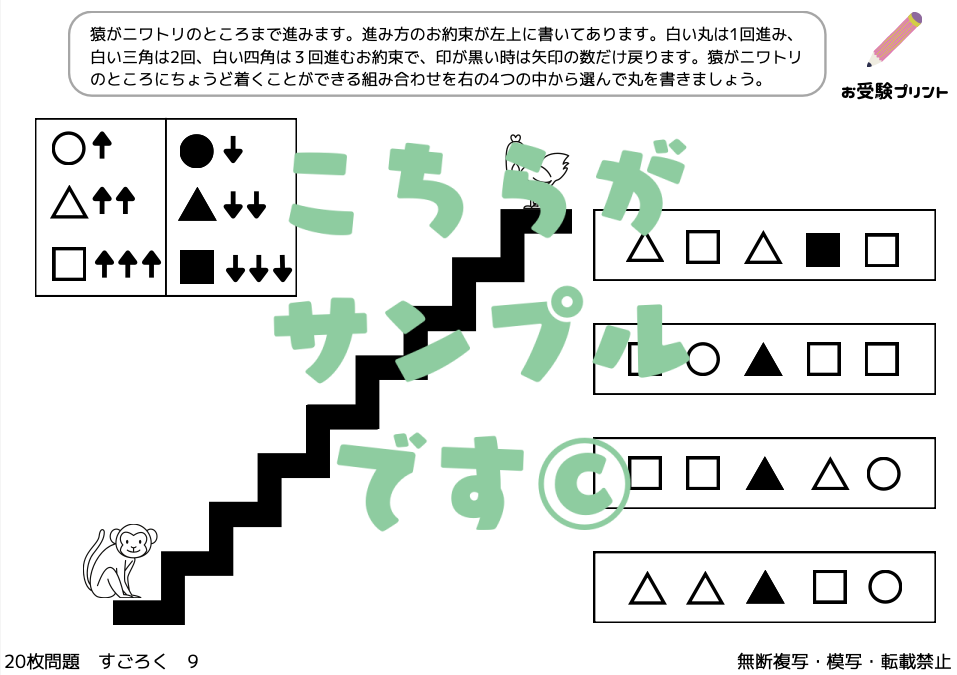
小学校受験で取り上げられる「すごろく」問題は、一般的な「サイコロを振ってその目の数だけ進む」という形式を基にした問題です。
一般的なすごろくではさまざまなものを使って進む数を決定するものもありますが、受験に使われるすごろくはほとんどの場合がサイコロを使った問題となります。
「すごろく」は、ただの遊びを超えて、算数や論理的思考の向上に大きな役割を果たします。
すごろく問題では、サイコロの目に基づいて進む位置や、その結果について答えるような内容が出題されます。
例えば、ある動物などのキャラクターがサイコロを振り、出た目の数だけ前に進み、キャラクターが到達したマスに印を付ける。
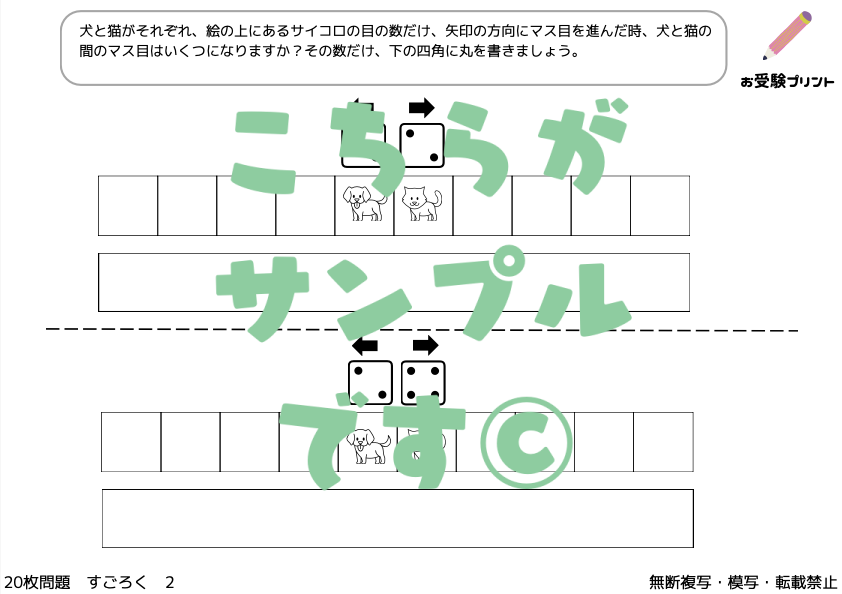
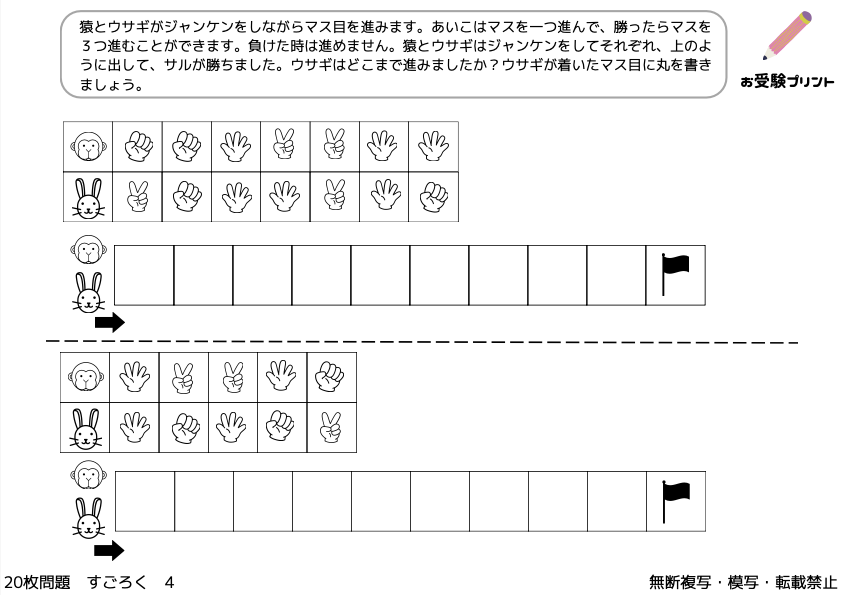
このような問題では、サイコロの出た数に従ってキャラクターを動かす必要があります。場合によっては複数のサイコロが使われることもあり、計算力や位置関係の理解が重要です。
他にも、特定の場所にたどり着いた結果をもとに、サイコロの目を推測する問題もあります。このタイプの問題は論理的な推論力と数に対する理解が必要となります。
言葉の問題は、子供たちが語彙力を伸ばし、言葉の理解を深めるための重要な手段です。しかし、これらの問題は、子供たちが苦労するポイントでもあります。
特に、新しい単語や表現に出会ったとき、その意味を理解し、適切な文脈で使用することは難しいかもしれません。そのため、教え方のポイントとしては、まずは子供たちが既に知っている単語や表現から始め、徐々に新しいものを導入することが重要です。また、言葉の問題を解く際には、音の認識、文章の理解、言葉の意味と使い方の理解など、さまざまなスキルが必要となります。
文章理解は、子供たちが文章を読み、その内容を理解し、それに基づいて適切な行動をとる能力を試す問題です。しかし、長い文章や複雑な表現に出会ったとき、子供たちはしばしば困惑します。そのため、教え方のポイントとしては、まずは短い文章から始め、徐々に長い文章や複雑な表現を導入することが重要です。また、しりとりは、子供たちが単語の最初と最後の音を認識し、それに基づいて新しい単語を思いつく能力を試すゲームです。これは、子供たちが言葉の音を認識し、それを使って新しい単語を生成する能力を鍛えるのに役立ちます。
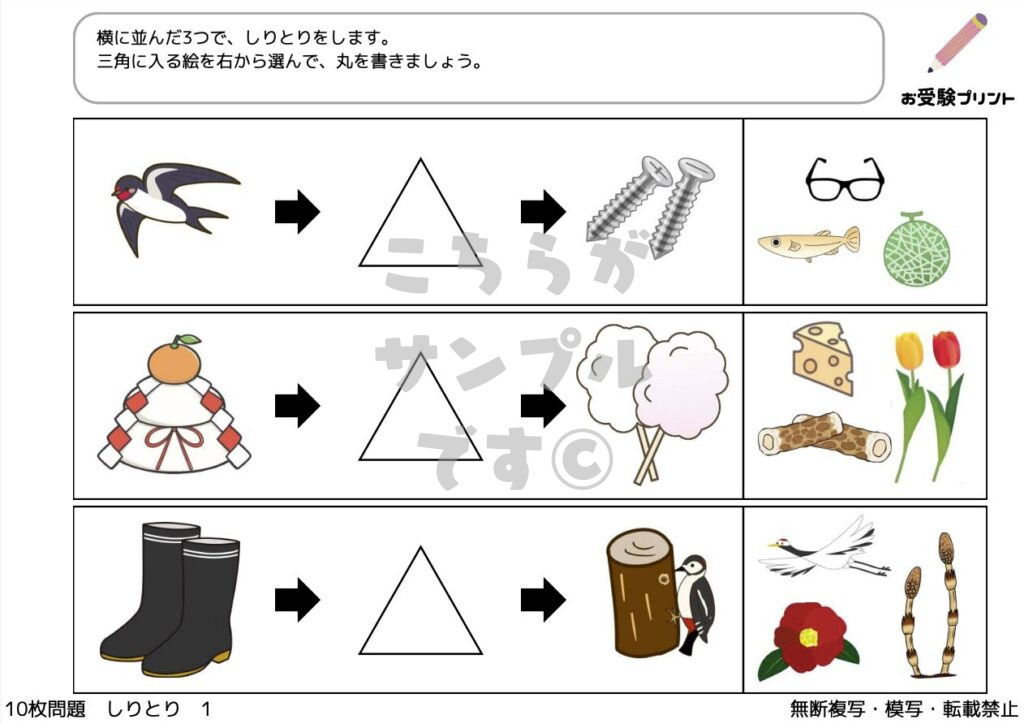
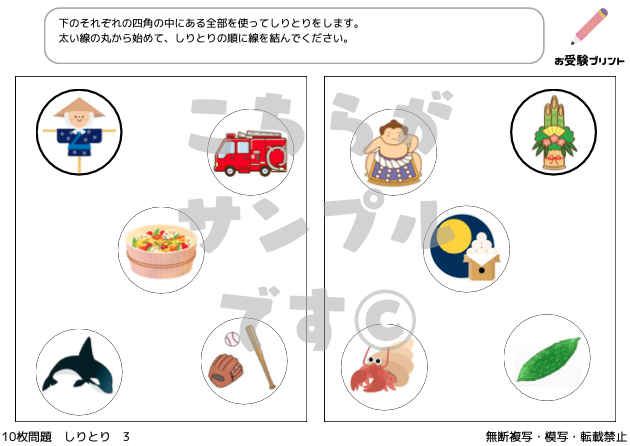
「しりとり問題」とは、小学校受験において子供たちの語彙力と思考力を試すための言語ゲームです。
この問題は、特定のルールに基づいて言葉を連鎖させることにより、子供たちの言語的な洞察力と記憶力を測定するのに役立ちます。
通常のしりとりは、一つの単語の最後の文字で始まる新しい単語を見つけるシンプルな形式ですが、受験ではより高度なバリエーションが求められることがあります。
例えば、「3文字しりとり」では、参加者は3文字の単語のみを使ってしりとりを行います。
また、「逆さしりとり」では、通常のしりとりとは逆に、単語の最初の文字を使って次の単語を見つけなければなりません。
これらの応用形式は、子供たちにとってはより高いレベルの語彙と思考の柔軟性を要求するため、小学校受験の準備には最適な練習方法となります。
また、しりとり問題は、単に語彙力だけでなく、クリエイティブな思考や言語の速度、そして流暢さも試されるため、子供たちの全般的な言語能力の発展に寄与します。
「お話しの記憶問題」とは、多くの小学校の受験問題として出題されるもので、受験生に対して短い物語や話が読み聞かせられ、その後、読まれた内容に関する質問がいくつか出されます。
質問は、物語の登場人物、起こった出来事、場所、物語の順序など、話の内容に密接に関連するものです。
このタイプの問題の目的は、子供たちの聞き取り能力、記憶力、理解力を評価することにあります。
また、話の細部に気を配り、重要な情報を抽出し記憶する能力も重要視されます。
これにより、話の中で何が起こったのかを正確に覚え、それに基づいて質問に答える必要があります。
常識問題は、子供たちが日々の生活の中で自然に学び取る知識を問うものです。しかし、これらの問題は一見すると簡単に見えるかもしれませんが、実際には子供たちが苦労するポイントがいくつか存在します。その一つは、具体的な事象や現象を抽象的な概念に結びつける能力が必要となることです。「季節」などの概念を理解し、それを具体的な状況に適用することは、子供たちにとっては難易度が高いかもしれません。
社会的な常識問題の一つに「季節」があります。これは、一年を四つの時期に分け、それぞれの特徴や行事、生活習慣などを理解することを求められます。しかし、子供たちが「季節」の概念を理解するためには、具体的な生活習慣や行事、自然の変化などを観察し、それを季節と結びつけることが必要です。そのため、季節ごとの特徴や行事、生活習慣などを具体的に教え、それを観察する機会を提供することが重要です。また、季節ごとの特徴を視覚的に理解するためには、季節ごとの絵本を読んだり、季節ごとの工作を行ったりすると良いでしょう。
小学校受験のペーパーテストは、子供たちの知識や思考力を多角的に試すものです。
この記事を通じて、6つの大項目それぞれの特徴や対策、そして子供たちがつまずきやすいポイントと我が家での学習ポイントを紹介させていただきました。
受験準備は一歩一歩、確実に進めることが大切です。
この記事が、受験を迎える子供たちとその保護者の皆様の参考となり、より良い結果を迎えるためのサポートとなれば幸いです。
最後までお読みいただき、ありがとうございました！
